力扣轨迹
害,不确定能不能进复试,进也是垫底太没安全感了,但还是得开始力扣刷题,进复试有算法笔试,春招也得写算法,两手抓了。
跟 代码随想录 的刷题方向开刷。
研究生复试逆袭成功~春招艰难就业季收获百度offer~ 没想到当初的迷茫害怕最后两手都很成功 -2023.9.8
前置知识
C++
vector
向量(Vector)是一个封装了动态大小数组的顺序容器(Sequence Container)。跟任意其它类型容器一样,它能够存放各种类型的对象。可以简单的认为,向量是一个能够存放任意类型的动态数组。
需要的头文件: #include
.push_back(x)就是在vector后面添加一个元素x
.pop_back()用以删除vector的尾元素
.size()用来获得vector中元素的个数
vector的定义的格式:
vector<typename> name;
vector<int> vec; //声明一个int型向量
vector<int> vec(5); //声明一个初始大小为5的int向量
vector<int> vec(10, 1); //声明一个初始大小为10且值都是1的向量
vector<int> vec(tmp); //声明并用tmp向量初始化vec向量
数组
int arr[5] = {1, 3, 4, 2, 5};
求数组长度:int len = sizeof(arr) / sizeof(arr[0]);
memset(arr, 0, sizeof(arr));
sort(arr, arr + 5);
输入行:
string a;
getchar(); //如果字符串前有数字,需要getchar()
getline(cin, a);
(str[i].substr(alen - a) == str[j].substr(0, a)) // substr(a) 返回从头开始删去a个字符后剩下的字符,substr(i,a)返回从下标i开始的a个字符
#include <bits/stdc++.h>
using namespace std;
int main()
{
map<string,int> mp; // key value
string str = "helloworld";
string st = "hello";
mp[str]=100;
mp[st]=10;
cout<<mp[str]<<endl; //100
cout<<mp[st]<<endl; //10
cout<<mp.count(str)<<endl; //存在则为 1,否则为 0
}
数组
数组内存空间是连续的,故删除和增加元素需要对数组地址进行移动。
删除元素 — 覆盖
二分查找
题里给出的数组是有序数组,都可以想一想是否可以使用二分法。
同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的。
二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
代码:
1、注意区间。
2、注意index的计算。
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1 ;
// int left = 0, right = nums.size() - 1;
while(left <= right){ //左闭右闭
int index = left + (right - left) / 2; // 计算index位置
int mid = nums[index];
if(mid > target){
right = index - 1;
}else if(mid < target){
left = index + 1;
}else{
return index;
}
}
return -1;
}
};
搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
代码:
target不存在时,通过right判断插入位置。
target大于mid值,插入位置应为index+1,此时right值仍为index
target小于mid值,插入位置应为index,此时right值为index-1
故最终right+1即可计算正确插入位置。
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while(left <= right){
int index = left + (right - left) / 2;
int mid = nums[index];
if(mid == target){
return index;
}else if(target > mid){
left = index + 1;
}else if(target < mid){
right = index - 1;
}
}
return right + 1;
}
};
在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
代码:
主要在于计算左右边界border(不包含在内)
- target存在时,继续修改left或者right值,再划分区间查找下一个target位置,并记录此时border值。最终return {leftBorder + 1, rightBorder -1}即可。
- target不存在时,border返回默认值-2,最终return {-1, -1}即可。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int leftBorder, rightBorder;
leftBorder = binarySearchBorder(nums, target, true);
rightBorder = binarySearchBorder(nums, target ,false);
if(leftBorder == -2 && rightBorder == -2) return {-1, -1};
return {leftBorder + 1, rightBorder -1};
}
int binarySearchBorder(vector<int>& nums, int target, bool isLeftBorder){
int left = 0, right = nums.size() - 1;
int border = -2;
while(left <= right){
int index = left + (right - left) / 2;
int mid = nums[index];
if(target > mid){
left = index + 1;
}else if(target < mid){
right = index - 1;
}else if(target == mid){
if(isLeftBorder == true){
right = index - 1;
border = right;
}else{
left = index + 1;
border = left;
}
}
}
return border;
}
};
移除元素
原地修改数组数值(移除元素)类型题目
法1:向前循环移动数组进行覆盖
法2:双指针法,快慢指针
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
代码:
暴力法:大循环找出val后,后面小循环向前移动覆盖val。
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int len = nums.size();
for(int i = 0; i < len; i++){
if(nums[i] == val){
for(int j = i; j < len - 1 ; j++)
{
nums[j] = nums [j+1];
}
i--;
len--;
}
}
return len;
}
};
双指针法:快慢指针一起共事,快指针进行探路,符合条件则快指针赋值慢指针,否则慢指针不移动。
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int len = nums.size();
int quick = 0,slow = 0;
for(;quick < len; quick++){
if(nums[quick] != val){
nums[slow] = nums[quick];
slow++;
}
}
return slow;
}
};
有序数组的平方
内部排序
- 快排 sort
- 双指针,首尾指针移动
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
代码:
暴力sort
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int len = nums.size();
for(int i = 0; i < len; i++){
nums[i]*=nums[i];
}
sort(nums.begin(),nums.end());
// sort(nums,nums + len);
return nums;
}
};
双指针法,首尾指针
平方过后最大值位于两侧,新开数组,从首尾开始判断并依次放入新数组末尾。
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int len = nums.size();
for(int i = 0; i < len; i++){
nums[i]*=nums[i];
}
vector<int> new_array(len);
int left = 0, right = len - 1;
while(left <= right){
if(nums[right] > nums[left]){
new_array[len - 1] = nums[right];
right--;
}else{
new_array[len - 1] = nums[left];
left++;
}
len--;
}
return new_array;
}
};
长度最小的子数组
找区间
1.暴力法 – 大小循环
2.滑动窗口
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
代码:
暴力法
大小循环依次找
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int length = INT32_MAX;
int size = nums.size();
for(int i = 0 ;i < size; i++){
int sum = 0;
int sub_length = 0;
for(int j = i; j < size; j++){
sum += nums[j];
sub_length++;
if(sum >= target && sub_length < length){
length = sub_length;
break;
}
}
}
return length == INT32_MAX ? 0 : length;
}
};
滑动窗口法
先不断增大right放大窗口,直至符合条件
再不断增大left缩小窗口,并计算最小长度,直至窗口不能符合为止
- 重复1、2。
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int size = nums.size();
int length = INT32_MAX;
int sum = 0;
int left = 0, right = 0;
for(; right < size; right++){
sum += nums[right];
while(sum >= target){
int sub_length = right - left + 1;
length = sub_length < length ? sub_length : length;
sum -= nums[left];
left++;
}
}
return length == INT32_MAX ? 0 : length;
}
};
螺旋矩阵II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
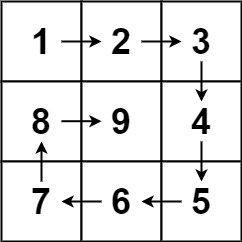
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
代码:
链表
移除链表元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
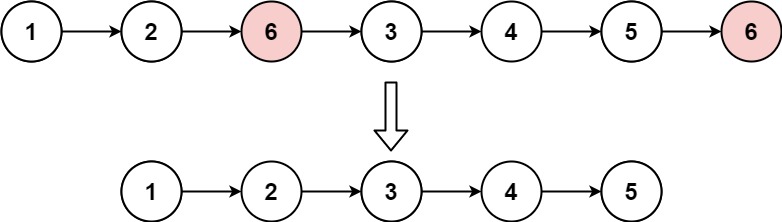
输入:head = [1,2,6,3,4,5,6], val = 6
输出:[1,2,3,4,5]
示例 2:
输入:head = [], val = 1
输出:[]
示例 3:
输入:head = [7,7,7,7], val = 7
输出:[]
代码:
注意设置一个虚拟头结点在进行移除节点操作
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode *dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode *now = dummyHead;
while(now != nullptr && now->next != nullptr){
if(now->next->val == val){
ListNode *tmp = now->next;
now->next = tmp->next;
delete tmp;
}else{
now = now->next;
}
}
ListNode *new_head = dummyHead->next;
delete dummyHead;
return new_head;
}
};
设计链表
设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:val 和 next。val 是当前节点的值,next 是指向下一个节点的指针/引用。如果要使用双向链表,则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。
在链表类中实现这些功能:
- get(index):获取链表中第
index个节点的值。如果索引无效,则返回-1。 - addAtHead(val):在链表的第一个元素之前添加一个值为
val的节点。插入后,新节点将成为链表的第一个节点。 - addAtTail(val):将值为
val的节点追加到链表的最后一个元素。 - addAtIndex(index,val):在链表中的第
index个节点之前添加值为val的节点。如果index等于链表的长度,则该节点将附加到链表的末尾。如果index大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。 - deleteAtIndex(index):如果索引
index有效,则删除链表中的第index个节点。
示例:
MyLinkedList linkedList = new MyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2); //链表变为1-> 2-> 3
linkedList.get(1); //返回2
linkedList.deleteAtIndex(1); //现在链表是1-> 3
linkedList.get(1); //返回3
反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:

输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:

输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
代码:
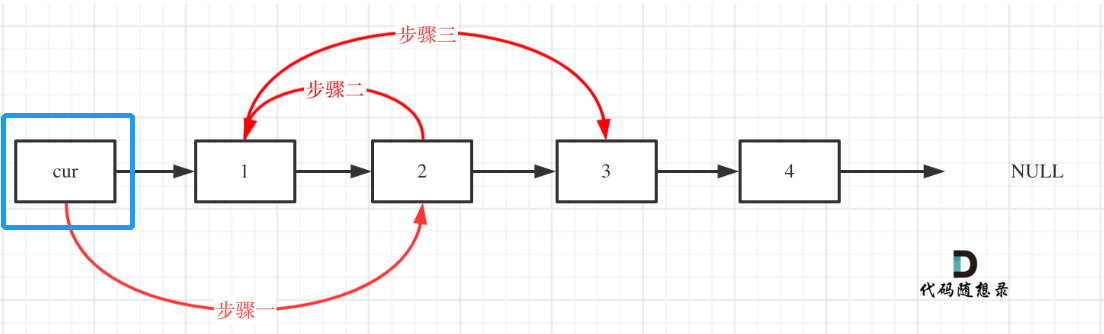
定义cur为当前结点,pre为前一结点,tmp为临时结点。
不断改变 cur->next 的指向pre
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode *tmp;
ListNode *cur = head;
ListNode *pre = nullptr;
while(cur){
tmp = cur->next;
cur->next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
};
两两交换链表中的节点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
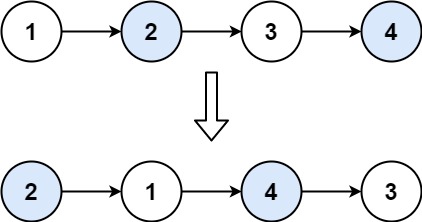
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
代码:
设置一个虚空头结点dummyHead,即可考虑只有头两个结点的情况,也可逐渐1、3、5、···· 的进行操作。
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode *dummyHead = new ListNode();
dummyHead->next = head;
ListNode *cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr){
ListNode *tmp1 = cur->next;
ListNode *tmp2 = cur->next->next;
cur->next = tmp2;
tmp1->next = tmp2->next;
tmp2->next = tmp1;
cur = cur->next->next;
}
return dummyHead->next;
}
};
删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
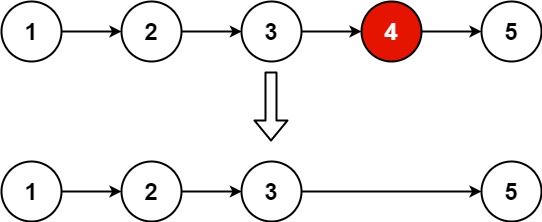
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
代码:
指针题一般设个虚头结点会方便操作。
本题要设置快慢指针,快指针先移动n+1步,保证慢指针指向目前位置的前一个位置。
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode *dummyHead = new ListNode();
dummyHead->next = head;
ListNode *quick = dummyHead;
ListNode *slow = dummyHead;
while(n-- && quick != nullptr){ //快指针先走n步
quick = quick->next;
}
quick = quick->next; //多走一步,让慢指针指向被删结点前一个
while(quick != nullptr){ //快慢指针一起走,直到快指针先到终点
quick = quick->next;
slow = slow->next;
}
slow->next = slow->next->next;
return dummyHead->next;
}
};
链表相交
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
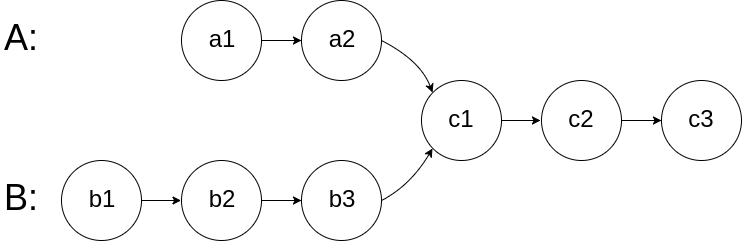
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
示例 1:
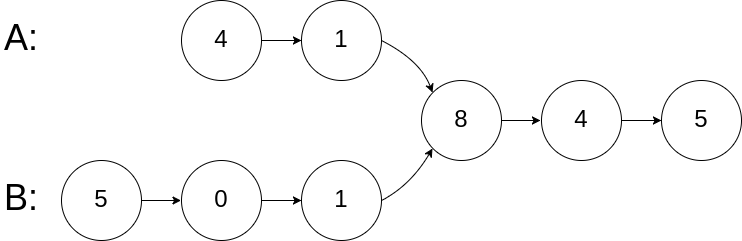
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
代码:
- 求出两链表长度
- 移动长链表的curA,使其与短链表末尾对齐
- 同时移动,判断两者指针是否相同
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0;
ListNode *curA = headA;
ListNode *curB = headB;
while(curA != NULL){
lenA++;
curA = curA ->next;
}
while(curB != NULL){
lenB++;
curB = curB ->next;
}
curA = headA;
curB = headB;
if (lenB > lenA) { //curA为最长链表的头,lenA为其长度
swap (lenA, lenB);
swap (curA, curB);
}
int gap = lenA - lenB;
while(gap--){
curA = curA->next;
}
ListNode *jiaodian = curA;
while(lenB--){
if(curA == curB){
return curA;
}
curA = curA->next;
curB = curB->next;
}
return NULL;
}
};
环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
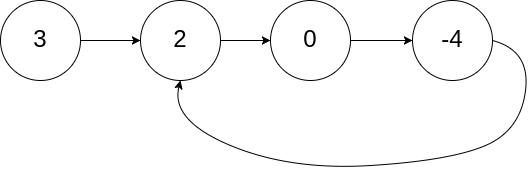
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
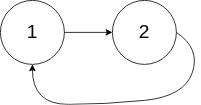
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
代码:
1.设置快慢指针,快指针走两步,慢指针走一步,如果有环,则快慢指针必会相遇。
2.有如此公式,x = (n – 1) (y + z) + z,从相遇点开始,头结点和相遇点同时再出发,其最终相遇地点就是环的入口。
x == z 或者x == z + 圈数
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast = head;
ListNode *slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
if(fast == slow){
ListNode *index1 = head; //重头出发一个
ListNode *index2 = fast; //相遇点出发一个
while(index1 !=index2){
index1 = index1->next;
index2 = index2->next;
}
return index1;
}
}
return NULL;
}
};
贪心算法
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
即能通过每次选最优,达到最终最优。
分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
代码:
先满足小胃口的孩子。
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int num = 0;
for(int i = 0; i < s.size() && num < g.size(); i++){ //遍历饼干
if(s[i] >= g[num]){ //胃口
num++;
}
}
return num;
}
};
摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
- 例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5]
输出:6
解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2:
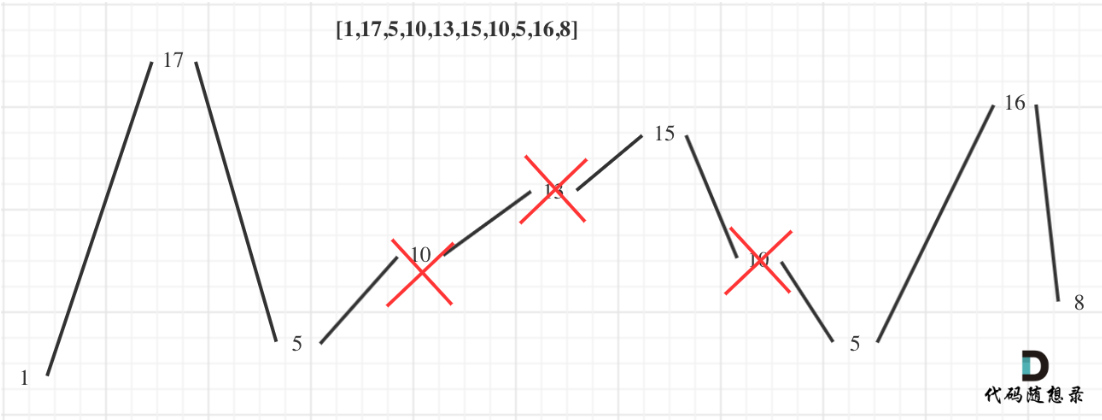
输入:nums = [1,17,5,10,13,15,10,5,16,8]
输出:7
解释:这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9]
输出:2
代码:
不断找顶峰,更新当前峰差值和前峰差值。
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if(nums.size() <= 1) return nums.size();
int pre = 0; // 默认最左边平峰
int cur = 0;
int num = 1; //默认右边一个峰值
for(int i = 1; i < nums.size(); i++){
cur = nums[i] - nums[i-1];
if((pre <=0 && cur > 0) || (pre >=0 && cur < 0)){
num++;
pre = cur;
}
}
return num;
}
};
最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
代码:
不断找找区间和大于0的区间,如果该区间和小于0,直接不管,在一直找到区间和大于0的区间。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int max_sum = INT32_MIN;
int cur_sum = 0;
for(int i = 0; i < nums.size(); i++){
cur_sum += nums[i];
if(cur_sum > max_sum) max_sum = cur_sum;
if(cur_sum < 0) cur_sum = 0;
}
return max_sum;
}
};
动态规划
如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的。这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
需要设置dp数组,后面的结果与前面的结果息息相关。
斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
代码:
重点在于dp数组的设置。
class Solution {
public:
int fib(int n) {
if(n<=1){
return n;
}
int dp[2];
dp[0] = 0;
dp[1] = 1;
for(int i = 2;i <= n; i++){
int sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return dp[1];
}
};
爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
代码:
dp:这一步的阶梯等于前两步和前一步的阶梯之和。
class Solution {
public:
int climbStairs(int n) {
int dp[50];
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i <= 45; i++){
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
};
// 空间复杂度O(1)
class Solution {
public:
int climbStairs(int n) {
if(n <= 2) return n;
int dp[2];
dp[0] = 1;
dp[1] = 2;
for(int i = 3; i <= n; i++){
int sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return dp[1];
}
};
使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
代码:
注意dp需要和cost相加,取最小。
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int dp[cost.size() + 1];
dp[0] = 0;
dp[1] = 0;
for(int i = 2; i <= cost.size(); i++){
dp[i] = min(dp[i-2] + cost[i-2], dp[i-1] + cost[i -1]);
}
return dp[cost.size()];
}
};
空间复杂度O(1)
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int dp[2];
dp[0] = 0;
dp[1] = 0;
for(int i = 2; i <= cost.size(); i++){
int min_cost = min(dp[0] + cost[i-2], dp[1] + cost[i -1]);
dp[0] = dp[1];
dp[1] = min_cost;
}
return dp[1];
}
};