入门算法训练题目
收录了我大二期间为了准备天梯赛而进行的入门算法训练题目,题目描述大多复制过来格式有些混乱,照题目复制在洛谷上应该能搜到原题。
我没记错的话我是花了差不多2个月时间从完全的算法小白开始刷起的,跟着B站大佬嘉持的教程将大部分常见算法类型的题目写一遍慢慢学的,前期很痛苦,因为很难想到做题思路,但越做到后面越进入状态,各种套路也开始熟悉,开始享受起做题的快感。
最后也取得了不错的天梯赛个人国三的成绩。现在回想起那天下午,每成功做完一道题后的成就感还是十分怀念呐,当时把能拿的分都拿了之后,我便开始等待比赛结束稳拿国三,但结果由于比赛开始时从网络问题导致大部分选手进不去官网,后面主办方便将比赛延迟半小时,而我也开始罚坐半小时,因为剩下的题为我还没学到的最高难度的图类型题。
[TOC]
C的小知识
1.Cpp精度
#include<iostream>
#include<iomanip>
using namespace std;
int main()
{
float value = 1.11;
cout << fixed << setprecision(4) << value << endl;
return 0;
}
2.左对齐,宽5格
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
int mp[5][5] = { {1,1,33},{2,2,888,},{3,3,999},{4,4},{5,5} };
for (int i = 0; i < 5; i++)
{
for (int j = 0; j < 5; j++)
{
cout << left << setw(5) << mp[i][j]; //左对宽
}
cout << endl;
}
return 0;
}
3.输入包含空格在内的字符串
#include <iostream>
#include<string>
#include<string.h>
using namespace std;
int main()
{
int k;
cin >> k;
string a;
getchar(); //如果字符串前有数字,需要getchar()
getline(cin, a);
cout << a << endl;
return 0;
}
4.总记不住闰年的SB我
bool islunar(int y)
{
if(y%4==0&&y%100!=0)
{
return true;
}else if(y%400==0)
{
return true;
}
return false;
}
5.substr()操作
(str[i].substr(alen - a) == str[j].substr(0, a)) // substr(a) 返回从头开始删去a个字符后剩下的字符,substr(i,a)返回从下标i开始的a个字符
6.char、int转string操作
int ww=12;
string tt = to_string(ww);
char pp='a';
string qq;
qq.push_back(pp);
string str = to_string(i); //貌似蓝桥不能用
to_string(i)
string str; //int 转 string
stringstream ss;
ss << i;
ss >> str;
ss.clear();
//cout<<str<<endl;
string str2 = "120"; //string 转 int
int num;
ss << str2;
ss >> num;
cout << num << endl;
7.Map知识
#include <iostream>
#include <string>
#include <bits/stdc++.h>
using namespace std;
int main()
{
map<string,int> mp; // key value
string str = "helloworld";
string st = "hello";
mp[str]=100;
mp[st]=10;
cout<<mp[str]<<endl; //100
cout<<mp[st]<<endl; //10
cout<<mp.count(str)<<endl; //存在则为 1,否则为 0
}
理解广度优先搜索 (BFS)
前言
参考视频教程https://www.bilibili.com/video/BV1AE411a7Wp?t=1
广度优先搜索 (BFS) – 类似队列的思想,先进先出。 搜过了的就不用再搜索了。
当题目要求最短步骤或路径时,就可考虑用BFS的思想。
以简单基础普及题型为例,可在洛谷上查找题目提交,代码仅供参考。
题目列表:
1.填涂颜色
2.马的遍历
3.奇怪的电梯
4.01迷宫
5.字串变换
6.机器人搬重物
1.填涂颜色
题目描述
由数字00组成的方阵中,有一任意形状闭合圈,闭合圈由数字11构成,围圈时只走上下左右44个方向。现要求把闭合圈内的所有空间都填写成2.例如:6×6的方阵(n=6),涂色前和涂色后的方阵如下:
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
输入格式
每组测试数据第一行一个整数n(1≤n≤30)
接下来n行,由0和1组成的n×n的方阵。
方阵内只有一个闭合圈,圈内至少有一个0。
输出格式
已经填好数字2的完整方阵。
输入输出样例
输入 #1复制
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
输出 #1复制
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
说明/提示
1≤n≤30
代码
#include<iostream>
#include<queue>
using namespace std;
int n;
int vis[40][40]; //记录访问节点
int mp[40][40]; //初始数据
int xx[] = { 0,0,1,-1 };
int yy[] = { 1,-1,0,0 };
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
cin >> mp[i][j];
}
}
queue<int> x;
queue<int> y;
x.push(0);
y.push(0);
while (!x.empty())
{
for (int i = 0; i < 4; i++)
{
int dx = x.front() + xx[i];
int dy = y.front() + yy[i];
if (dx >= 0 && dx <= n + 1 && dy >= 0 && dy <= n + 1 && mp[dx][dy] != 1 && vis[dx][dy] == 0)
{
x.push(dx);
y.push(dy);
vis[dx][dy] = 1;
}
}
x.pop();
y.pop();
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (vis[i][j] == 0 && mp[i][j] != 1)
{
cout << "2";
}
else
{
cout << mp[i][j];
}
cout << " ";
}
cout << endl;
}
return 0;
}
2.马的遍历
题目描述
有一个n*m的棋盘(1<n,m<=400),在某个点上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步
输入格式
一行四个数据,棋盘的大小和马的坐标
输出格式
一个n*m的矩阵,代表马到达某个点最少要走几步(左对齐,宽5格,不能到达则输出-1)
输入输出样例
输入 #1复制
3 3 1 1
输出 #1复制
0 3 2
3 -1 1
2 1 4
代码
#include <iostream>
#include <bits/stdc++.h>
#include <queue>
using namespace std;
int mp[420][420];
int xx[] = { 1,2,2,1,-1,-2,-2,-1 }; //马的移动需要知道
int yy[] = { 2,1,-1,-2,-2,-1,1,2 };
struct node
{
int x, y, t;
};
int main()
{
int n, m, sx, sy;
cin >> n >> m >> sx >> sy;
memset(mp, -1, sizeof(mp));
queue<node> q;
node p;
p.x = sx;
p.y = sy;
p.t = 0;
q.push(p);
mp[sx][sy] = 0;
while (!q.empty())
{
for (int i = 0; i < 8; i++)
{
int dx = q.front().x + xx[i];
int dy = q.front().y + yy[i];
if (dx >= 1 && dx <= n && dy >= 1 && dy <= m && mp[dx][dy] == -1)
{
mp[dx][dy] = q.front().t + 1;
node temp;
temp.x = dx;
temp.y = dy;
temp.t = mp[dx][dy];
q.push(temp); // 或者直接强制转换 q.push((node){dx,dy,mp[dx][dy]});
}
}
q.pop();
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cout << left << setw(5) << mp[i][j]; //左对宽
}
cout << endl;
}
return 0;
}
3.奇怪的电梯
题目描述
呵可,有一天我做了一个梦,梦见了一种很奇怪的电梯。大楼的每一层楼都可以停电梯,而且第i层楼(1≤i≤N)上有一个数字K1(0≤压1≤N)。电梯只有四个按钮:开,关,上,下。上下的层数等于 当前楼层上的那个数字。当然,如果不能满足要求,相应的按钮就会失灵。例如:3,3,1,2,5代表了K1(压1=3K2=3,),从1楼开始。在1楼,按“上”可以到4楼,按”下”是不起作用的,因为没有-2 楼。那么,从A楼到B楼至少要按几次按钮呢?
输入格式
共二行。
第一行为3个用空格隔开的正整数,表示N,A,B(1≤N≤200, 1≤A,B≤N)N,A,B(1≤N≤200,1≤A,B≤N)。
第二行为N个用空格隔开的非负整数,表示Ki。
输出格式
一行,即最少按键次数,若无法到达,则输出−1。
输入输出样例
输入 #1复制
5 1 5
3 3 1 2 5
输出 #1复制
3
代码
#include <iostream>
#include <queue>
using namespace std;
int y[205];
int vis[205]; //防止返回
int main()
{
int n, a, b;
cin >> n >> a >> b;
for (int i = 1; i <= n; i++)
{
cin >> y[i];
}
queue<int> s;
queue<int> bs;
s.push(a);
bs.push(0);
while (!s.empty())
{
if (s.front() == b)
{
cout << bs.front() << endl;
return 0;
}
int ss = s.front() + y[s.front()];
if (ss <= n && vis[ss] == 0)
{
s.push(ss);
bs.push(bs.front() + 1);
vis[ss] = 1;
}
int ss2 = s.front() - y[s.front()];
if (ss2 >= 1 && vis[ss2] == 0)
{
s.push(ss2);
bs.push(bs.front() + 1);
vis[ss2] = 1;
}
s.pop();
bs.pop();
}
cout << "-1" << endl;
return 0;
}
4.01迷宫
题目描述
有一个仅由数字0与1组成的n×n格迷宫。若你位于一格0上,那么你可以移动到相邻4格中的某一格1上,同样若你位于一格1上,那么你可以移动到相邻4格中的某一格0上。
你的任务是:对于给定的迷宫,询问从某一格开始能移动到多少个格子(包含自身)。
输入格式
第11行为两个正整数n,m。
下面n行,每行n个字符,字符只可能是0或者1,字符之间没有空格。
接下来m行,每行2个用空格分隔的正整数i,j,对应了迷宫中第i行第j列的一个格子,询问从这一格开始能移动到多少格。
输出格式
m行,对于每个询问输出相应答案。
输入输出样例
输入 #1复制
2 2
01
10
1 1
2 2
输出 #1复制
4
4
代码
#include <iostream>
#include <queue>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int n, m;
int mp[maxn][maxn];
int vis[maxn][maxn];
int color;
int cnt = 0;
int ans[1000010]; //记录每种颜色可移动的格子数
int xx[] = { 0,1,0,-1 };
int yy[] = { 1,0,-1,0 };
void bfs(int x, int y)
{
queue<int> h;
queue<int> l;
h.push(x);
l.push(y);
vis[x][y] = color; //同一块的区域涂颜色
while (!h.empty())
{
for (int i = 0; i < 4; i++)
{
int dx = h.front() + xx[i];
int dy = l.front() + yy[i];
if (dx <= n && dx >= 1 && dy <= n && dy >= 1 && !vis[dx][dy] && mp[dx][dy] != mp[h.front()][l.front()])
{
vis[dx][dy] = color;
h.push(dx);
l.push(dy);
}
}
h.pop();
l.pop();
cnt++; //用来记录每次弹出的次数,即可移动的格子数
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
char k; //注意是输入字符间无空格
cin >> k;
if (k == '1')
{
mp[i][j] = 1;
}
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (!vis[i][j])
{
color++;
bfs(i, j);
ans[color] = cnt;
cnt = 0;
}
}
}
for (int i = 1; i <= m; i++)
{
int h, l;
cin >> h >> l;
cout << ans[vis[h][l]] << endl;
}
return 0;
}
5.字串变换
题目描述
已知有两个字串 A,B及一组字串变换的规则(至多 6 个规则):
A1 ->B1
A2 -> B2
规则的含义为:在 A 中的子串 A1 可以变换为 B1,A2 可以变换为B2 …。
例如:A=abcd,B=xyz,
变换规则为:
abc→xu,ud→y,y→yz
则此时,A 可以经过一系列的变换变为 B*,其变换的过程为:
abcd→xud→xy→xyz。
共进行了 3次变换,使得 A变换为 B。
输入格式
输入格式如下:
AB
A1 B1
A2B2 |-> 变换规则
… …/
所有字符串长度的上限为 2020。
输出格式
若在 10 步(包含 10 步)以内能将 A 变换为 B,则输出最少的变换步数;否则输出 NO ANSWER!
输入输出样例
输入 #1复制
abcd xyz
abc xu
ud y
y yz
输出 #1复制
3
代码
#include <iostream>
#include <bits/stdc++.h>
#include <queue>
#include <string>
using namespace std;
map<string, int> mp; //神奇工具~ ,记录每个字符串是否为访问过
int main()
{
string a, b;
cin >> a >> b;
string aa[10], bb[10];
int n = 1;
while (cin >> aa[n] >> bb[n])
{
n++;
}
n--;
queue<string> w;
queue<int> bs;
w.push(a);
bs.push(0);
while (!w.empty())
{
if (w.front() == b)
{
cout << bs.front() << endl;
return 0;
}
if (bs.front() == 10)
{
bs.pop();
w.pop();
}
string tt = w.front();
if (mp.count(tt)) // tt 是否出现 ,1 为出现,0为否 ,出现过就没必要继续查它了
{
w.pop();
bs.pop();
continue;
}
mp[tt] = 1;
for (int i = 1; i <= n; i++)
{
int p = 0;
while (tt.find(aa[i], p) <= tt.length()) //从 tt 的下标 p 开始查找a[i],找到则返回找到的第一个字母位置,找不到则返回一个很大的值
{
p = tt.find(aa[i], p);
w.push(tt.substr(0, p) + bb[i] + tt.substr(p + aa[i].length()));
bs.push(bs.front() + 1);
p++; // p++往下移一位继续搜寻 tt 中等于 aa[i] 的片段
}
}
w.pop();
bs.pop();
}
cout << "NO ANSWER!" << endl;
return 0;
}
6.机器人搬重物
题目描述
机器人移动学会(RMI)现在正尝试用机器人搬运物品。机器人的形状是一个直径1.6米的球。在试验阶段,机器人被用于在一个储藏室中搬运货物。储藏室是一个 N×M 的网格,有些格子为不可移动的障碍。机器人的中心总是在格点上,当然,机器人必须在最短的时间内把物品搬运到指定的地方。机器人接受的指令有:向前移动1步(Creep);向前移动2步(Walk);向前移动33 步(Run);向左转(Left);向右转(Right)。每个指令所需要的时间为1 秒。请你计算一下机器人完成任务所需的最少时间。
输入格式
第一行为两个正整数N,M(N,M≤50),下面N行是储藏室的构造,0表示无障碍,1表示有障碍,数字之间用一个空格隔开。接着一行有4个整数和1个大写字母,分别为起始点和目标点左上角网格的行与列,起始时的面对方向(东E,南S,西W,北N),数与数,数与字母之间均用一个空格隔开。终点的面向方向是任意的。
输出格式
一个整数,表示机器人完成任务所需的最少时间。如果无法到达,输出-1。
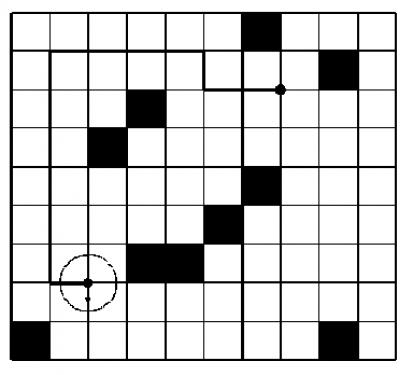
输入输出样例
输入 #1复制
9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 S
输出 #1复制
12
代码
#include <iostream>
#include <bits/stdc++.h>
#include <queue>
using namespace std;
bool mp[60][60];
bool vis[60][60][5]; //方向也要标记
int xx[] = { 0,1,0,-1 };
int yy[] = { 1,0,-1,0 };
struct dian
{
int x, y, t, fx;
};
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
int temp;
cin >> temp;
if (temp == 1)
{
mp[i][j] = mp[i - 1][j] = mp[i][j - 1] = mp[i - 1][j - 1] = 1; //注意是一个方格子上的四个点,这想法妙哇
}
}
}
int sx, sy, fx, fy;
char w;
cin >> sx >> sy >> fx >> fy >> w;
dian d;
d.x = sx; d.y = sy; d.t = 0;
if (w == 'E') d.fx = 0; //将字母方向匹配上移动方向数组
if (w == 'S') d.fx = 1;
if (w == 'W') d.fx = 2;
if (w == 'N') d.fx = 3;
queue<dian> q;
vis[d.x][d.y][d.fx] = 1;
q.push(d);
while (!q.empty())
{
dian temp = q.front();
if (temp.x == fx && temp.y == fy)
{
cout << temp.t;
return 0;
}
temp.t++;
temp.fx = (q.front().fx + 1) % 4; //记得取余
if (!vis[temp.x][temp.y][temp.fx])
{
vis[temp.x][temp.y][temp.fx] = 1;
q.push(temp);
}
temp.fx = (q.front().fx + 3) % 4;
if (!vis[temp.x][temp.y][temp.fx])
{
vis[temp.x][temp.y][temp.fx] = 1;
q.push(temp);
}
temp.fx = q.front().fx;
int run = 3;
while (run--) //慢慢一步步走
{
temp.x += xx[temp.fx];
temp.y += yy[temp.fx];
if (!vis[temp.x][temp.y][temp.fx] && !mp[temp.x][temp.y] && temp.x >= 1 && temp.x < n && temp.y >= 1 && temp.y < m)
{
vis[temp.x][temp.y][temp.fx] = 1;
q.push(temp);
}
else
{
break;
}
}
q.pop();
}
cout << "-1";
return 0;
}
理解深度优先搜索 (DFS) 、递归
前言
参考视频教程 https://www.bilibili.com/video/BV14E411q73d?p=3
理解深度优先搜索 (DFS) 、递归 – 跟栈差不多,先进后出的思想。一条路一直走,不能走就返回上一步看能否走另一条,能就走,不能就再返回上一步,如此下去。
以简单基础普及题型为例,可在洛谷上查找题目提交,代码仅供参考。
题目列表:
1.全排列问题
2.八皇后问题
3.迷宫
4.单词方阵
5.单词接龙
6.加分二叉树
7.虫食算
8.迷宫问题
1.全排列问题
题目描述
输出自然数 1 到 n所有不重复的排列,即 n 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
输入格式
一个整数 n。
输出格式
由 1 ∼n 组成的所有不重复的数字序列,每行一个序列。
每个数字保留 5 个场宽。
输入输出样例
输入 #1复制
3
输出 #1复制
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int n;
int vis[10];
int a[10];
void dfs(int i) //这个 i 可认为是第几个数字
{
if (i > n)
{
for (int j = 1; j <= n; j++)
{
cout << " " << a[j];
}
cout << endl;
}
else
{
for (int j = 1; j <= n; j++)
{
if (vis[j] == 0)
{
vis[j] = 1;
a[i] = j;
dfs(i + 1);
vis[j] = 0;
}
}
}
}
int main()
{
cin >> n;
dfs(1);
return 0;
}
2.八皇后问题
题目描述
一个如下的 6×6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。

上面的布局可以用序列 2 4 6 1 3 5 来描述,第 i个数字表示在第 i 行的相应位置有一个棋子,如下:
行号1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 3个解。最后一行是解的总个数。
输入格式
一行一个正整数 nn,表示棋盘是 n×n* 大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
输入输出样例
输入 #1复制
6
输出 #1复制
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
代码
#include <iostream>
using namespace std;
int n;
int cnt;
int lie[20]; //判断用同一列是否存在数
int a[20];
int youxia[50]; //右斜差为定值 ,需要考虑负值的情况 !很有用的知识!
int zuoxia[20]; //左斜和为定值 !
void pr()
{
if (cnt <= 3)
{
for (int i = 1; i < n; i++)
{
cout << a[i] << " ";
}
cout << a[n] << endl;
}
}
void dfs(int i)
{
if (i > n)
{
cnt++;
pr();
}
else
{
for (int j = 1; j <= n; j++)
{
if (lie[j] == 0 && youxia[j - i + n] == 0 && zuoxia[j + i] == 0)
{
lie[j] = 1;
youxia[j - i + n] = 1;
zuoxia[j + i] = 1;
a[i] = j;
dfs(i + 1);
lie[j] = 0;
youxia[j - i + n] = 0;
zuoxia[j + i] = 0;
}
}
}
}
int main()
{
cin >> n;
dfs(1);
cout << cnt << endl;
}
3.迷宫
题目背景
给定一个N*M方格的迷宫,迷宫里有T处障碍,障碍处不可通过。给定起点坐标和终点坐标,问: 每个方格最多经过1次,有多少种从起点坐标到终点坐标的方案。在迷宫中移动有上下左右四种方式,每次只能移动一个方格。数据保证起点上没有障碍。
题目描述
无
输入格式
第一行N、M和T,N为行,M为列,T为障碍总数。第二行起点坐标SX,SY,终点坐标FX,FY。接下来T行,每行为障碍点的坐标。
输出格式
给定起点坐标和终点坐标,问每个方格最多经过1次,从起点坐标到终点坐标的方案总数。
输入输出样例
输入 #1复制
2 2 1
1 1 2 2
1 2
输出 #1复制
1
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int n, m, t, sx, sy, fx, fy, cnt;
int vis[20][20];
int zhangai[20][20];
int xx[] = { 0,0,-1,1 }; //用于上下左右移动
int yy[] = { -1,1,0,0 }; //用于上下左右移动
void dfs(int x, int y)
{
if (x == fx && y == fy)
{
cnt++;
}
else
{
for (int i = 0; i < 4; i++)
{
int dx = x + xx[i]; //注意不能直接 x = x + xx[i] ,否则会影响下次循环,哭了
int dy = y + yy[i];
if (vis[dx][dy] == 0 && zhangai[dx][dy] == 0 && dx >= 1 && dy >= 1 && dx <= m && dy <= n) //记得考虑边界问题
{
vis[dx][dy] = 1;
dfs(dx, dy);
vis[dx][dy] = 0;
}
}
}
}
int main()
{
cin >> n >> m >> t;
cin >> sx >> sy >> fx >> fy;
for (int i = 0; i < t; i++)
{
int x, y;
cin >> x >> y;
zhangai[x][y] = 1;
}
vis[sx][sy] = 1;
dfs(sx, sy);
cout << cnt << endl;
}
4.单词方阵 —这题不能算递归dfs
题目描述
给一n×n*的字母方阵,内可能蕴含多个“yizhong”单词。单词在方阵中是沿着同一方向连续摆放的。摆放可沿着 8 个方向的任一方向,同一单词摆放时不再改变方向,单词与单词之间可以交叉,因此有可能共用字母。输出时,将不是单词的字母用*代替,以突出显示单词。例如:
输入:
8 输出:
qyizhong *yizhong
gydthkjy gy******
nwidghji n*i*****
orbzsfgz o**z****
hhgrhwth h***h***
zzzzzozo z****o**
iwdfrgng i*****n*
yyyygggg y******g
输入格式
第一行输入一个数n。(7≤n≤100)。
第二行开始输入n×n的字母矩阵。
输出格式
突出显示单词的n×n矩阵。
输入输出样例
输入 #2复制
8
qyizhong
gydthkjy
nwidghji
orbzsfgz
hhgrhwth
zzzzzozo
iwdfrgng
yyyygggg
输出 #2复制
*yizhong
gy******
n*i*****
o**z****
h***h***
z****o**
i*****n*
y******g
代码
#include<iostream>
using namespace std;
int n;
char str[120][120];
int vis[120][120];
char word[] = "yizhong";
int xx[] = { 0,1,1,1,0,-1,-1,-1 }; //注意包括斜方向
int yy[] = { -1,-1,0,1,1,1,0,-1 };
void xunhuan(int x, int y)
{
for (int i = 0; i < 8; i++) //每个方向
{
int flag = 1;
for (int j = 0; j < 7; j++) //一步步走
{
int dx = x + j * xx[i];
int dy = y + j * yy[i];
if (str[dx][dy] != word[j] || dx<1 || dy<1 || dx>n || dy>n)
{
flag = 0;
break;
}
}
if (flag)
{
for (int j = 0; j < 7; j++)
{
int dx = x + j * xx[i];
int dy = y + j * yy[i];
vis[dx][dy] = 1;
}
}
}
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
cin >> str[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (str[i][j] == 'y')
{
xunhuan(i, j);
}
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (vis[i][j])
{
cout << str[i][j];
}
else
{
cout << "*";
}
}
cout << endl;
}
}
5.单词接龙
题目描述
单词接龙是一个与我们经常玩的成语接龙相类似的游戏,现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”(每个单词都最多在“龙”中出现两次),在两个单词相连时,其重合部分合为一部分,例如 beast 和 astonish,如果接成一条龙则变为 beastonish,另外相邻的两部分不能存在包含关系,例如 at 和 atide 间不能相连。
输入格式
输入的第一行为一个单独的整数 n表示单词数,以下 n 行每行有一个单词,输入的最后一行为一个单个字符,表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在。
输出格式
只需输出以此字母开头的最长的“龙”的长度。
输入输出样例
输入 #1复制
5
at
touch
cheat
choose
tact
a
输出 #1复制
23
说明/提示
样例解释:连成的“龙”为 atoucheatactactouchoose。
n≤20
代码
#include <iostream>
#include <string>
using namespace std;
string str[100];
int vis[100];
int maxx = 0;
int n;
void dfs(int i, int len)
{
maxx = max(len, maxx);
for (int j = 0; j < n; j++)
{
int alen, blen;
int a = 1;
alen = str[i].length();
blen = str[j].length();
while (a < min(alen, blen))
{
if (str[i].substr(alen - a) == str[j].substr(0, a) && vis[j] < 2) // substr(a) 为从头开始删去a个后返回剩下的字符,substr(0,a)返回从头开始的a个字符
{
int lenn = len + blen - a; //千万别直接 len += blen - a 啊,又哭了 ,又死在这里一次了
vis[j]++;
dfs(j, lenn);
vis[j]--;
break;
}
a++;
}
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> str[i];
}
char w;
cin >> w;
for (int i = 0; i < n; i++)
{
if (str[i][0] == w)
{
vis[i]++;
dfs(i, str[i].length());
vis[i]--;
}
}
cout << maxx << endl;
return 0;
}
6.加分二叉树
题目描述
设一个m个节点的二叉树tree的中序遍历为(1,2,3,,n),其中数字1,2,3,为节点编号。每个节点都有一个分数(均为正整数),记第う个节点的分数为d,tree及它的每个子树都有一个加分,任一棵子树 subtree(也包含tree本身)的加分计算方法如下:
subtree的左子树的加分 x subtree的右子树的加分+ subtree的根的分数。
若某个子树为空,规定其加分为1,叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3、)且加分最高的二又树tree要求输出
1.tree的最高加分。
2.tree的前序遍历。
输入格式
第 1 行 1 个整数 n,为节点个数。
第 2行 n个用空格隔开的整数,为每个节点的分数
输出格式
第 1行 1个整数,为最高加分(Ans≤4,000,000,000)。
第 2行 n个用空格隔开的整数,为该树的前序遍历。
输入输出样例
输入 #1复制
5
5 7 1 2 10
输出 #1复制
145
3 1 2 4 5
代码
#include<iostream>
using namespace std; //不断找每个区间的最合适根
int n, a[40];
int root[40][40];
long long dp[40][40]; //用于减少时间 ,记住已存取的区间最大值 ,下次可以用取,就不用再计算。记忆化。
long long dfs(int l, int r)
{
if (l == r)
{
return a[l];
}
if (dp[l][r])
{
return dp[l][r]; //这里跟上面的其实可以合并
}
if (l > r)
{
return 1; //假如左子树或右 子树为空
}
int maxx = 0;
for (int i = l; i <= r; i++)
{
long long temp = dfs(l, i - 1) * dfs(i + 1, r) + a[i];
if (temp > maxx)
{
maxx = temp;
root[l][r] = i; //记住每个区间的最合适根结点
}
}
return dp[l][r] = maxx;
}
void dg(int l, int r)
{
if (l > r)
{
return;
}
cout << root[l][r] << " ";
dg(l, root[l][r] - 1);
dg(root[l][r] + 1, r);
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
root[i][i] = i;
dp[i][i] = i;
}
cout << dfs(1, n) << endl;
dg(1, n);
return 0;
}
7.虫食算
题目描述
所谓虫食算,就是原先的算式中有一部分被虫子啃掉了,需要我们根据剩下的数字来判定被啃掉的字母。来看一个简单的例子:
43#9865#045
+ 8468#6633
44445509678
其中 # 号代表被虫子啃掉的数字。根据算式,我们很容易判断:第一行的两个数字分别是 5和 3,第二行的数字是 5。
现在,我们对问题做两个限制:
首先,我们只考虑加法的虫食算。这里的加法是 n进制加法,算式中三个数都有 n位,允许有前导的 0。
其次,虫子把所有的数都啃光了,我们只知道哪些数字是相同的,我们将相同的数字用相同的字母表示,不同的数字用不同的字母表示。如果这个算式是 nn 进制的,我们就取英文字母表的前 n 个大写字母来表示这个算式中的 0到 n – 1这 n个不同的数字:但是这 n个字母并不一定顺序地代表 0到 n-1。输入数据保证 n 个字母分别至少出现一次。
BADC
+CBDA
DCCC
上面的算式是一个4进制的算式。很显然,我们只要让 ABCD 分别代表 0123,便可以让这个式子成立了。你的任务是,对于给定的 n进制加法算式,求出 n个不同的字母分别代表的数字,使得该加法算式成立。输入数据保证有且仅有一组解。
输入格式
输入的第一行是一个整数 n,代表进制数。
第二到第四行,每行有一个由大写字母组成的字符串,分别代表两个加数以及和。这 3个字符串左右两端都没有空格,从左到右依次代表从高位到低位,并且恰好有 n位。
输出格式
输出一行 n个用空格隔开的整数,分别代表 A,B,… 代表的数字。
输入输出样例
输入 #1复制
5
ABCED
BDACE
EBBAA
输出 #1复制
1 0 3 4 2
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int n;
int vis[30], a[30]; //a 用来记住字母代表的数字
int v[4][30]; // 保存字母
void dfs(int y, int x, int t)
{
for (int i = 1; i <= n; i++) //提前预测判断,免得再递归,减少时间
{
if (a[v[1][i]] != -1 && a[v[2][i]] != -1 && a[v[3][i]] != -1)
{
if (a[v[3][i]] != (a[v[1][i]] + a[v[2][i]]) % n && a[v[3][i]] != (a[v[2][i]] + a[v[1][i]] + 1) % n)
{
return;
}
}
}
if (x > n)
{
for (int i = 0; i < n; i++)
{
cout << a[i] << " ";
}
return;
}
int m = v[y][x];
if (y <= 2)
{
if (a[m] != -1)
{
dfs(y + 1, x, t);
}
else
{
for (int i = 0; i < n; i++)
{
if (vis[i] == 0)
{
a[m] = i;
vis[i] = 1;
dfs(y + 1, x, t);
a[m] = -1;
vis[i] = 0;
}
}
}
}
else if (y == 3)
{
t += a[v[y - 1][x]] + a[v[y - 2][x]];
if (a[m] != -1)
{
if (a[m] == t % n) //记得取模
{
dfs(1, x + 1, t / n); //记得判断进位
}
}
else
{
if (a[m] == -1 && vis[t % n] == 0)
{
a[m] = t % n;
vis[t % n] = 1;
dfs(1, x + 1, t / n); //记得判断进位
a[m] = -1;
vis[t % n] = 0;
}
}
}
}
int main()
{
cin >> n;
memset(a, -1, sizeof(a)); //这个 memset 只能赋 0 和 -1
for (int i = 1; i <= 3; i++)
{
for (int j = n; j >= 1; j--)
{
char m;
cin >> m;
v[i][j] = m - 'A'; //将字母转数字
}
}
dfs(1, 1, 0);
return 0;
}
8.迷宫问题
题目描述
定义一个二维数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
输入
一个5 × 5的二维数组,表示一个迷宫。数据保证有唯一解。
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出
左上角到右下角的最短路径,格式如样例所示。
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)
代码
#include <iostream>
using namespace std;
int mp[6][6];
bool vis[6][6];
int xx[] = { 0,1,0,-1 };
int yy[] = { -1,0,1,0 };
int maxx;
struct node
{
int x;
int y;
}no[50], lu[50]; //需要用到结构体来保存数据辽
void dfs(int x, int y, int bs)
{
if (x == 4 && y == 4 && bs < maxx)
{
maxx = bs;
for (int i = 0; i < bs; i++)
{
lu[i].x = no[i].x;
lu[i].y = no[i].y;
}
}
for (int i = 0; i < 4; i++)
{
int dx = x + yy[i];
int dy = y + xx[i];
if (dx <= 4 && dx >= 0 && dy <= 4 && dy >= 0 && mp[dx][dy] == 0 && vis[dx][dy] == 0)
{
no[bs].x = dx;
no[bs].y = dy;
vis[dx][dy] = 1;
dfs(dx, dy, bs + 1);
vis[dx][dy] = 0;
}
}
}
int main()
{
for (int i = 0; i < 5; i++)
{
for (int j = 0; j < 5; j++)
{
cin >> mp[i][j];
}
}
no[0].x = 0;
no[0].y = 0;
vis[0][0] = 1;
maxx = 100000;
dfs(0, 0, 1);
for (int i = 0; i < maxx; i++)
{
cout << "(" << lu[i].x << ", " << lu[i].y << ")" << endl;
}
return 0;
}
9.键盘替换
题目描述
键盘坏了QAQ,会时不时的自动按下Home键和END键,你能告诉我敲击后的文本长什么样子嘛 T^T
输入
测试数据有多组,每组包括一行字符串(长度 <= 105),其中'[‘代表敲击了Home键,’]’代表敲击了END键
输出
对于每组数据输出敲击后的文本
样例输入
This_is_a_[Beiju]_text
[[]][][][][]Happy_Birthday_to_Tsinghua_University
样例输出
BeijuThis_is_a__text
Happy_Birthday_to_Tsinghua_University
代码
#include <iostream>
#include <cstring>
using namespace std;
string str;
void dfs(int l, int r)
{
int you = r;
for(;you>=l;you--)
{
if(str[you]=='['||str[you]==']')
{
break;
}
}
if(str[you]==']') //两个中跑一个,']'先递归再输出后面的数
{
dfs(l,you-1);
}
for(int i=you+1;i<=r;i++)
{
cout<<str[i];
}
if(str[you]=='[') //两个中跑一个,'['先输出后面的数再递归
{
dfs(l,you-1);
}
}
int main()
{
while(cin>>str)
{
int len = str.size();
dfs(0,len-1);
cout<<endl;
}
return 0;
}
递推与递归二分
前言
参考视频教程洛谷试练场 普及组 递推与递归二分
重在找规律
以简单基础普及题型为例,可在洛谷上查找题目提交,代码 **仅供参考。
题目列表:
1.P1192 台阶问题
2.P1025 [NOIP2001 提高组] 数的划分
3.P1057 [NOIP2008 普及组] 传球游戏
4.P1216 [USACO1.5][IOI1994]数字三角形 Number Triangles
1.P1192 台阶问题
题目描述
有NN级的台阶,你一开始在底部,每次可以向上迈最多KK级台阶(最少11级),问到达第NN级台阶有多少种不同方式。
输入格式
两个正整数N,K。
输出格式
一个正整数,为不同方式数,由于答案可能很大,你需要输出ans \bmod 100003ansmod100003后的结果。
输入输出样例
输入 #1复制
5 2
输出 #1复制
8
说明/提示
对于20\%20%的数据,有N ≤ 10, K ≤ 3N≤10,K≤3;
对于40\%40%的数据,有N ≤ 1000N≤1000;
对于100\%100%的数据,有N ≤ 100000,K ≤ 100N≤100000,K≤100。
代码
#include <iostream>
using namespace std;
int n, k, a[100010] = { 1 };
int main()
{
cin >> n >> k;
for (int i = 1; i <= k; i++)
{
for (int j = 0; j < i; j++)
{
a[i] += a[j]; //从每一台阶上一步
a[i] %= 100003;
}
}
for (int i = k + 1; i <= n; i++)
{
for (int j = i - k; j < i; j++)
{
a[i] += a[j]; //从每一台阶上一步
a[i] %= 100003;
}
}
cout << a[n];
return 0;
}
2.P1025 [NOIP2001 提高组] 数的划分
题目描述
将整数nn分成kk份,且每份不能为空,任意两个方案不相同(不考虑顺序)。
例如:n=7n=7,k=3k=3,下面三种分法被认为是相同的。
1,1,51,1,5;
1,5,11,5,1;
5,1,15,1,1.
问有多少种不同的分法。
输入格式
n,kn,k (6<n \le 2006<n≤200,2 \le k \le 62≤k≤6)
输出格式
11个整数,即不同的分法。
输入输出样例
输入 #1复制
7 3
输出 #1复制
4
说明/提示
四种分法为:
1,1,51,1,5;
1,2,41,2,4;
1,3,31,3,3;
2,2,32,2,3.
代码
#include <iostream>
using namespace std;
int n, k;
long long f[211][211];
int main()
{
cin >> n >> k;
for (int i = 1; i <= k; i++)
{
for (int j = 1; j <= n; j++)
{
if (i == j)
{
f[i][j] = 1;
}
else if (j > i)
{
f[i][j] = f[i - 1][j - 1] + f[i][j - i]; //减一个苹果和一个盘子 + 减去盘子个数的苹果数量
}
}
}
cout << f[k][n];
return 0;
}
3.P1057 [NOIP2008 普及组] 传球游戏
题目描述
上体育课的时候,小蛮的老师经常带着同学们一起做游戏。这次,老师带着同学们一起做传球游戏。
游戏规则是这样的:nn个同学站成一个圆圈,其中的一个同学手里拿着一个球,当老师吹哨子时开始传球,每个同学可以把球传给自己左右的两个同学中的一个(左右任意),当老师再次吹哨子时,传球停止,此时,拿着球没有传出去的那个同学就是败者,要给大家表演一个节目。
聪明的小蛮提出一个有趣的问题:有多少种不同的传球方法可以使得从小蛮手里开始传的球,传了mm次以后,又回到小蛮手里。两种传球方法被视作不同的方法,当且仅当这两种方法中,接到球的同学按接球顺序组成的序列是不同的。比如有三个同学11号、22号、33号,并假设小蛮为11号,球传了33次回到小蛮手里的方式有11->22->33->11和11->33->22->11,共22种。
输入格式
一行,有两个用空格隔开的整数n,m(3 \le n \le 30,1 \le m \le 30)n,m(3≤n≤30,1≤m≤30)。
输出格式
11个整数,表示符合题意的方法数。
输入输出样例
输入 #1复制
3 3
输出 #1复制
2
说明/提示
40%的数据满足:3 \le n \le 30,1 \le m \le 203≤n≤30,1≤m≤20
100%的数据满足:3 \le n \le 30,1 \le m \le 303≤n≤30,1≤m≤30
代码
#include <iostream>
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
int d[33][33]={1}; //d[0][0]=1; d[i][j] i为传的次数 j为人
for(int i=1;i<=m;i++)
{
for(int j=0;j<n;j++) //从 0 开始比较好取余
{
d[i][j] = d[i-1][(j-1+n)%n] + d[i-1][(j+1)%n]; // 等于 前一次的左右两边同学相加,(j-1+n)%n 注意 +n !!
}
}
cout<<d[m][0];
return 0;
}
3.P1135 奇怪的电梯
题目描述
呵呵,有一天我做了一个梦,梦见了一种很奇怪的电梯。大楼的每一层楼都可以停电梯,而且第ii层楼(1 \le i \le N)(1≤i≤N)上有一个数字K_i(0 \le K_i \le N)Ki(0≤Ki≤N)。电梯只有四个按钮:开,关,上,下。上下的层数等于当前楼层上的那个数字。当然,如果不能满足要求,相应的按钮就会失灵。例如:3, 3 ,1 ,2 ,53,3,1,2,5代表了K_i(K_1=3,K_2=3,…)Ki(K1=3,K2=3,…),从11楼开始。在11楼,按“上”可以到44楼,按“下”是不起作用的,因为没有-2−2楼。那么,从AA楼到BB楼至少要按几次按钮呢?
输入格式
共二行。
第一行为33个用空格隔开的正整数,表示N,A,B(1≤N≤200, 1≤A,B≤N)N,A,B(1≤N≤200,1≤A,B≤N)。
第二行为NN个用空格隔开的非负整数,表示K_iKi。
输出格式
一行,即最少按键次数,若无法到达,则输出-1−1。
输入输出样例
输入 #1复制
5 1 5
3 3 1 2 5
输出 #1复制
3
代码
#include <iostream>
#include <queue>
using namespace std;
int n, a, b, d[2200][210], k[210]; //d[i][j] i 代表到某阶层的次数,j代表阶层
int main()
{
cin >> n >> a >> b;
for (int i = 1; i <= n; i++)
{
cin >> k[i];
}
if (a == b)
{
cout << "0";
return 0;
}
d[0][a] = 1;
for (int i = 0; i < 2100; i++)
{
for (int j = 1; j <= n; j++)
{
if (d[i][j] == 1)
{
if (j + k[j] <= n)
d[i + 1][j + k[j]] = 1;
if (j - k[j] >= 1)
d[i + 1][j - k[j]] = 1;
if (j - k[j] == b || j + k[j] == b)
{
cout << i + 1;
return 0;
}
continue;
}
}
}
cout << "-1";
return 0;
}
4.P1216 [USACO1.5][IOI1994]数字三角形 Number Triangles
题目描述 **
观察下面的数字金字塔。
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
在上面的样例中,从 7 \to 3 \to 8 \to 7 \to 57→3→8→7→5 的路径产生了最大
输入格式 **
第一个行一个正整数 rr ,表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出格式 **
单独的一行,包含那个可能得到的最大的和。
输入输出样例 **
输入 #1复制
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出 #1复制
30
说明/提示 **
【数据范围】
对于 100\%100% 的数据,1\le r \le 10001≤r≤1000,所有输入在 [0,100][0,100] 范围内。
代码 **
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int r, n[1010][1010], d[1010][1010];
int main()
{
cin >> r;
for (int i = 1; i <= r; i++)
{
for (int j = 1; j <= i; j++)
{
cin >> n[i][j];
}
}
for (int i = r; i >= 1; i--) //从下往上推 ,找出每行每个点与下面和的最大值
{
for (int j = 1; j <= i; j++)
{
d[i][j] = max(d[i + 1][j], d[i + 1][j + 1]) + n[i][j];
}
}
cout << d[1][1];
return 0;
}
动态规划之简单入门题
前言
参考视频教程NOIP 洛谷题单【动态规划1】动态规划的引入
还是需要慢慢理解。
以简单基础普及题型为例,可在洛谷上查找题目提交,代码仅供参考。
题目列表:
1.P2196 [NOIP1996 提高组] 挖地雷
2.P4017 最大食物链计数
3.P1802 5倍经验日
1.P2196 [NOIP1996 提高组] 挖地雷
题目描述
在一个地图上有NN个地窖(N \le 20)(N≤20),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。
输入格式
有若干行。
第11行只有一个数字,表示地窖的个数NN。
第22行有NN个数,分别表示每个地窖中的地雷个数。
第33行至第N+1N+1行表示地窖之间的连接情况:
第33行有n-1n−1个数(00或11),表示第一个地窖至第22个、第33个、…、第nn个地窖有否路径连接。如第33行为1 1 0 0 0 … 011000…0,则表示第11个地窖至第22个地窖有路径,至第33个地窖有路径,至第44个地窖、第55个、…、第nn个地窖没有路径。
第44行有n-2n−2个数,表示第二个地窖至第33个、第44个、…、第nn个地窖有否路径连接。
… …
第n+1n+1行有11个数,表示第n-1n−1个地窖至第nn个地窖有否路径连接。(为00表示没有路径,为11表示有路径)。
输出格式
有两行
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。
第二行只有一个数,表示能挖到的最多地雷数。
输入输出样例
输入 #1复制
5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1
输出 #1复制
1 3 4 5
27
代码
#include <iostream>
#include <math.h>
using namespace std;
int n, a[30], mp[30][30], dp[30], maxn, qian, q[30];
int p;
void dfs(int index)
{
if (index == 0)
return;
dfs(q[index]);
cout << index << " ";
}
void dfs2(int x, int sum, int pp)
{
if (maxn < sum)
{
maxn = sum;
p = pp;
}
maxn = max(sum, maxn);
for (int i = 1; i <= n; i++)
{
if (x == 0 || mp[x][i])
{
dfs2(i, sum + a[i], pp + pow(2, i - 1));
}
}
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
dp[i] = a[i];
}
for (int i = 1; i < n; i++)
{
for (int j = i + 1; j <= n; j++)
{
cin >> mp[i][j];
}
}
//dfs2(0,0,0);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j < i; j++) // 1没得找,2从1找,3从12中找,4从123中找,5从1234中找
{
if (mp[j][i])
{
if (dp[i] < dp[j] + a[i])
{
dp[i] = dp[j] + a[i];
q[i] = j;
}
}
}
if (maxn < dp[i])
{
maxn = dp[i];
qian = i;
}
}
dfs(qian);
// for(int i=1;i<=n;i++) //用二进制方法记位
// {
// if(p%2==1)
// {
// cout<<i<<" ";
// }
// p/=2;
// }
cout << endl << maxn;
return 0;
}
2.P4017 最大食物链计数
题目描述
给你一个食物网,你要求出这个食物网中最大食物链的数量。
(这里的“最大食物链”,指的是生物学意义上的食物链,即最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者。)
Delia 非常急,所以你只有 11 秒的时间。
由于这个结果可能过大,你只需要输出总数模上 8011200280112002 的结果。
输入格式
第一行,两个正整数 n、mn、m,表示生物种类 nn 和吃与被吃的关系数 mm。
接下来 mm 行,每行两个正整数,表示被吃的生物A和吃A的生物B。
输出格式
一行一个整数,为最大食物链数量模上 8011200280112002 的结果。
输入输出样例
输入 #1复制
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4
输出 #1复制
5
说明/提示
各测试点满足以下约定:

代码
#include<iostream>
using namespace std;
int n, m, mp[5005][5005], bc[5005], cc[5005], r[5005];
long long modd = 80112002;
int dfs(int x)
{
if (cc[x] == 0) //说明到最左端
{
return 1; //则返回一条食物链
}
int sum = 0;
if (r[x])
{
return r[x];
}
for (int i = 1; i <= n; i++)
{
if (mp[i][x] == 1) //说明 i 可以被 x 吃
{
sum = (sum + dfs(i)) % modd;
}
}
return r[x] = sum; //记录 x 的最大链数
}
int main()
{
cin >> n >> m;
while (m--)
{
int beichi, chi;
cin >> beichi >> chi;
mp[beichi][chi] = 1;
bc[beichi]++; //用于判断每种生物的食物链数量,及最低级和最高级
cc[chi]++;
}
int maxx;
for (int i = 1; i <= n; i++)
{
if (bc[i] == 0) //说明最右端
{
maxx = (maxx + dfs(i)) % modd;
}
}
cout << maxx << endl;
return 0;
}
3.P1802 5倍经验日
题目描述
现在absi2011拿出了x个迷你装药物(嗑药打人可耻….),准备开始与那些人打了
由于迷你装一个只能管一次,所以absi2011要谨慎的使用这些药,悲剧的是,没到达最少打败该人所用的属性药了他打人必输>.<所以他用2个药去打别人,别人却表明3个药才能打过,那么相当于你输了并且这两个属性药浪费了。
现在有n个好友,有输掉拿的经验、赢了拿的经验、要嗑几个药才能打过。求出最大经验(注意,最后要乘以5)
输入格式
第一行两个数,n和x
后面n行每行三个数,分别表示输了拿到的经验(lose[i])、赢了拿到的经验(win[i])、打过要至少使用的药数量(use[i])。
输出格式
一个整数,最多获得的经验
输入输出样例
输入 #1复制
6 8
21 52 1
21 70 5
21 48 2
14 38 3
14 36 1
14 36 2
输出 #1复制
1060
说明/提示
【Hint】
五倍经验活动的时候,absi2011总是吃体力药水而不是这种属性药>.<
【数据范围】
对于10%的数据,保证x=0
对于30%的数据,保证n<=10,x<=20
对于60%的数据,保证n<=100,x<=100, 10<=lose[i], win[i]<=100,use[i]<=5
对于100%的数据,保证n<=1000,x<=1000,0<lose[i]<=win[i]<=1000000,0<=use[i]<=1000
代码
#include <iostream>
using namespace std;
int n, x, lose[1010], win[1010], use[1010];
long long dp[1010]; //注意long long
int main()
{
cin >> n >> x;
for (int i = 1; i <= n; i++)
{
cin >> lose[i] >> win[i] >> use[i];
}
for (int i = 1; i <= n; i++)
{
for (int j = x; j >= 0; j--)
{
if (j >= use[i])
{
dp[j] = max(dp[j] + lose[i], dp[j - use[i]] + win[i]);
}
else
{
dp[j] = dp[j] + lose[i];
}
}
}
cout << dp[x] * 5;
return 0;
}
动态规划之背包问题的一些基础简单入门题
前言
参考视频教程洛谷试练场 普及组 动态规划的背包问题

主要有01背包问题、完全背包问题、分组背包问题。
01背包问题一般从右往左推;
完全背包问题一般从左往右推;
分组背包一般用01的方法但需要记得分组;
还是需要慢慢理解。
以简单基础普及题型为例,可在洛谷上查找题目提交,代码仅供参考。
题目列表:
1.P1048 [NOIP2005 普及组] 采药
2.P1060 [NOIP2006 普及组] 开心的金明
3.P1049 [NOIP2001 普及组] 装箱问题
4.P1164 小A点菜
5.P1734 最大约数和
6.P1510 精卫填海
7.P1466 [USACO2.2]集合 Subset Sums
8.P1616 疯狂的采药
9.P1679 神奇的四次方数
10.P1757 通天之分组背包
11.P1064 [NOIP2006 提高组] 金明的预算方案
1.P1048 [NOIP2005 普及组] 采药
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有 22 个整数 TT(1 \le T \le 10001≤T≤1000)和 MM(1 \le M \le 1001≤M≤100),用一个空格隔开,TT 代表总共能够用来采药的时间,MM 代表山洞里的草药的数目。
接下来的 MM 行每行包括两个在 11 到 100100 之间(包括 11 和 100100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
输入输出样例
输入 #1复制
70 3
71 100
69 1
1 2
输出 #1复制
3
说明/提示
【数据范围】
- 对于 30\%30% 的数据,M \le 10M≤10;
- 对于全部的数据,M \le 100M≤100。
代码
#include <iostream>
using namespace std;
int t, m, tt[105], money[105], dp[1005];
int main()
{
cin >> t >> m;
for (int i = 1; i <= m; i++)
{
cin >> tt[i] >> money[i];
}
for (int i = 1; i <= m; i++)
{
for (int j = t; j >= tt[i]; j--)
{
dp[j] = max(dp[j - tt[i]] + money[i], dp[j]);
}
}
cout << dp[t];
}
2.P1060 [NOIP2006 普及组] 开心的金明
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过NN元钱就行”。今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的NN元。于是,他把每件物品规定了一个重要度,分为55等:用整数1-51−5表示,第55等最重要。他还从因特网上查到了 每件物品的价格(都是整数元)。他希望在不超过NN元(可以等于NN元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第jj件物品的价格为v[j]v[j],重要度为w[j]w[j],共选中了kk件物品,编号依次为j_1,j_2,…,j_kj1,j2,…,jk,则所求的总和为:
v[j_1] \times w[j_1]+v[j_2] \times w[j_2]+ …+v[j_k] \times w[j_k]v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]。
请你帮助金明设计一个满足要求的购物单。
输入格式
第一行,为22个正整数,用一个空格隔开:n,mn,m(其中N(<30000)N(<30000)表示总钱数,m(<25)m(<25)为希望购买物品的个数。)
从第22行到第m+1m+1行,第jj行给出了编号为j-1j−1的物品的基本数据,每行有22个非负整数v pvp(其中vv表示该物品的价格(v \le 10000)(v≤10000),pp表示该物品的重要度(1-51−5)
输出格式
11个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(<100000000)(<100000000)。
输入输出样例
输入 #1复制
1000 5
800 2
400 5
300 5
400 3
200 2
输出 #1复制
3900
代码
#include <iostream>
using namespace std;
int n, m, v[30], w[30], dp[30010];
int main()
{
cin >> n >> m; //跟上面一题同样思路
for (int i = 1; i <= m; i++)
{
cin >> v[i] >> w[i];
}
for (int i = 1; i <= m; i++)
{
for (int t = n; t >= v[i]; t--)
{
dp[t] = max(dp[t - v[i]] + v[i] * w[i], dp[t]);
}
}
cout << dp[n];
}
3.P1049 [NOIP2001 普及组] 装箱问题
题目描述
有一个箱子容量为VV(正整数,0 \le V \le 200000≤V≤20000),同时有nn个物品(0<n \le 300<n≤30,每个物品有一个体积(正整数)。
要求nn个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
输入格式
11个整数,表示箱子容量
11个整数,表示有nn个物品
接下来nn行,分别表示这nn个物品的各自体积
输出格式
11个整数,表示箱子剩余空间。
输入输出样例
输入 #1复制
24
6
8
3
12
7
9
7
输出 #1复制
0
代码
#include <iostream>
using namespace std;
int v, n, t[35], dp[20020];
//int vis[35];
//int maxx;
//void dfs(int sum)
//{
// for(int i=1;i<=n;i++)
// {
// if(vis[i]==1)
// {
// continue;
// }else
// {
// vis[i]=1;
// if(sum+t[i]<=v)
// {
// maxx = max(maxx,sum+t[i]);
// }else
// {
// vis[i]=0;
// continue;
// }
// dfs(sum+t[i]);
// vis[i]=0;
// }
// }
//}
int main()
{
cin >> v;
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> t[i];
}
for (int i = 1; i <= n; i++)
{
for (int j = v; j >= t[i]; j--)
{
dp[j] = max(dp[j - t[i]] + t[i], dp[j]);
if (dp[j] == v)
{
cout << "0";
return 0;
}
}
}
cout << v - dp[v];
return 0;
// for(int i=1;i<=n;i++) //尝试用递归的方法做,超时
// {
// vis[i]=1;
// dfs(t[i]);
// vis[i]=0;
// }
// cout<<v-maxx;
}
4.P1164 小A点菜
题目背景
uim神犇拿到了uoi的ra(镭牌)后,立刻拉着基友小A到了一家……餐馆,很低端的那种。
uim指着墙上的价目表(太低级了没有菜单),说:“随便点”。
题目描述
不过uim由于买了一些辅(e)辅(ro)书,口袋里只剩MM元(M \le 10000)(M≤10000)。
餐馆虽低端,但是菜品种类不少,有NN种(N \le 100)(N≤100),第ii种卖a_iai元(a_i \le 1000)(ai≤1000)。由于是很低端的餐馆,所以每种菜只有一份。
小A奉行“不把钱吃光不罢休”,所以他点单一定刚好吧uim身上所有钱花完。他想知道有多少种点菜方法。
由于小A肚子太饿,所以最多只能等待11秒。
输入格式
第一行是两个数字,表示NN和MM。
第二行起NN个正数a_iai(可以有相同的数字,每个数字均在10001000以内)。
输出格式
一个正整数,表示点菜方案数,保证答案的范围在intint之内。
输入输出样例
输入 #1复制
4 4
1 1 2 2
输出 #1复制
3
代码
#include <iostream>
using namespace std; //这题理解不透彻
int n, m, a[1010], dp[10010][10010];
int dpp[10010] = { 1 }; //方案数肯定有一个 ,但我另一个方法又可以过,有点懵
int sum;
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
for (int i = 1; i <= n; i++)
{
for (int j = m; j >= a[i]; j--)
{
dpp[j] = dpp[j] + dpp[j - a[i]]; //有点难理解,就是方案数等于当前方案数加上剩下的钱的方案数
}
}
// for(int i=1;i<=n;i++)
// {
// for(int j=1;j<=m;j++)
// {
// if(a[i]<j) //当前菜品价格小于花费钱数 ,则可以方案数加上剩下钱的方案数
// dp[i][j]=dp[i-1][j]+dp[i-1][j-a[i]];
// if(a[i]==j) //当前菜品价格等于花费钱数 ,则方案加一
// dp[i][j]=dp[i-1][j]+1;
// if(a[i]>j) //当前菜品价格等于花费钱数 ,则方案不变
// dp[i][j]=dp[i-1][j];
// }
// }
// cout<<dp[n][m];
cout << dpp[m];
}
5.P1734 最大约数和
题目描述
选取和不超过S的若干个不同的正整数,使得所有数的约数(不含它本身)之和最大。
输入格式
输入一个正整数S。
输出格式
输出最大的约数之和。
输入输出样例
输入 #1复制
11
输出 #1复制
9
说明/提示
样例说明
取数字4和6,可以得到最大值(1+2)+(1+2+3)=9。
数据规模
S<=1000
代码
#include <iostream>
using namespace std;
int s, v[1010], dp[1010];
int main()
{
cin >> s;
for (int i = 1; i <= s; i++)
{
for (int j = 1; j < i; j++)
{
if (i % j == 0)
{
v[i] += j;
}
}
}
for (int i = 1; i <= s; i++)
{
for (int j = s; j >= i; j--)
{
dp[j] = max(dp[j], dp[j - i] + v[i]); //突然就不是很理解了 2021.4.11 17:12
}
}
cout << dp[s];
}
6.P1510 精卫填海
问题描述
发鸠之山,其上多柘木。有鸟焉,其状如乌,文首,白喙,赤足,名曰精卫,其名自詨。是炎帝之少女,名曰女娃。女娃游于东海,溺而不返,故为精卫。常衔西山之木石,以堙于东海。——《山海经》
精卫终于快把东海填平了!只剩下了最后的一小片区域了。同时,西山上的木石也已经不多了。精卫能把东海填平吗?
事实上,东海未填平的区域还需要至少体积为v的木石才可以填平,而西山上的木石还剩下n块,每块的体积和把它衔到东海需要的体力分别为k和m。精卫已经填海填了这么长时间了,她也很累了,她还剩下的体力为c。
输入格式
输入文件的第一行是三个整数:v、n、c。
从第二行到第n+1行分别为每块木石的体积和把它衔到东海需要的体力。
输出格式
输出文件只有一行,如果精卫能把东海填平,则输出她把东海填平后剩下的最大的体力,否则输出’Impossible’(不带引号)。
输入输出样例
输入 #1复制
100 2 10
50 5
50 5
输出 #1复制
0
输入 #2复制
10 2 1
50 5
10 2
输出 #2复制
Impossible
说明/提示
【数据范围】
对于20%的数据,0<n<=50。
对于50%的数据,0<n<=1000。
对于100%的数据,0<n<=10000,所有读入的数均属于[0,10000],最后结果<=c。
代码
#include <iostream>
using namespace std;
int v, n, c, tj[10010], li[10010], dp[100101];
int main()
{
cin >> v >> n >> c;
for (int i = 1; i <= n; i++)
{
cin >> tj[i] >> li[i];
}
for (int i = 1; i <= n; i++)
{
for (int j = c; j >= li[i]; j--) //以 力 为衡量
{
dp[j] = max(dp[j], dp[j - li[i]] + tj[i]);
}
}
for (int i = 1; i <= c; i++)
{
if (dp[i] >= v)
{
cout << c - i;
return 0;
}
}
cout << "Impossible";
return 0;
}
7.P1466 [USACO2.2]集合 Subset Sums
题目描述
对于从 1\sim n1∼n 的连续整数集合,能划分成两个子集合,且保证每个集合的数字和是相等的。举个例子,如果 n=3n=3,对于 {1,2,3}{1,2,3} 能划分成两个子集合,每个子集合的所有数字和是相等的:
{3}{3} 和 {1,2}{1,2} 是唯一一种分法(交换集合位置被认为是同一种划分方案,因此不会增加划分方案总数)
如果 n=7n=7,有四种方法能划分集合 {1,2,3,4,5,6,7 }{1,2,3,4,5,6,7},每一种分法的子集合各数字和是相等的:
{1,6,7}{1,6,7} 和 {2,3,4,5}{2,3,4,5}
{2,5,7}{2,5,7} 和 {1,3,4,6}{1,3,4,6}
{3,4,7}{3,4,7} 和 {1,2,5,6}{1,2,5,6}
{1,2,4,7}{1,2,4,7} 和 {3,5,6}{3,5,6}
给出 nn,你的程序应该输出划分方案总数。
输入格式
输入文件只有一行,且只有一个整数 nn
输出格式
输出划分方案总数。
输入输出样例
输入 #1复制
7
输出 #1复制
4
说明/提示
【数据范围】
对于 100\%100% 的数据,1\le n \le 391≤n≤39。
代码
#include <iostream>
using namespace std;
long long dp[10010] = { 1 }; //注意默认有一个方案
int main()
{
int n;
cin >> n;
int m = (1 + n) * n / 2;
if (m % 2 == 1)
{
cout << "0";
return 0;
}
for (int i = 1; i <= n; i++)
{
for (int j = m / 2; j >= i; j--)
{
dp[j] = dp[j] + dp[j - i];
}
}
cout << dp[m / 2] / 2;
return 0;
}
8.P1616 疯狂的采药
题目描述
LiYuxiang 是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同种类的草药,采每一种都需要一些时间,每一种也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是 LiYuxiang,你能完成这个任务吗?
此题和原题的不同点:
-
每种草药可以无限制地疯狂采摘。
-
药的种类眼花缭乱,采药时间好长好长啊!师傅等得菊花都谢了!
输入格式
输入第一行有两个整数,分别代表总共能够用来采药的时间 tt 和代表山洞里的草药的数目 mm。
第 22 到第 (m + 1)(m+1) 行,每行两个整数,第 (i + 1)(i+1) 行的整数 a_i, b_iai,bi 分别表示采摘第 ii 种草药的时间和该草药的价值。
输出格式
输出一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
输入输出样例
输入 #1复制
70 3
71 100
69 1
1 2
输出 #1复制
140
说明/提示
数据规模与约定
- 对于 30\%30% 的数据,保证 m \le 10^3m≤103 。
- 对于 100\%100% 的数据,保证 1 \leq m \le 10^41≤m≤104,1 \leq t \leq 10^71≤t≤107,且 1 \leq m \times t \leq 10^71≤m×t≤107,1 \leq a_i, b_i \leq 10^41≤ai,bi≤104。
代码
#include <iostream>
using namespace std; //完全背包问题
long long t, m, a[1000010], b[1000010], dp[10000010];
int main()
{
cin >> t >> m;
for (long long i = 1; i <= m; i++)
{
cin >> a[i] >> b[i];
}
for (long long i = 1; i <= m; i++)
{
for (long long j = a[i]; j <= t; j++) //完全背包从左往右
{
dp[j] = max(dp[j], dp[j - a[i]] + b[i]);
}
}
cout << dp[t];
return 0;
}
9.P1679 神奇的四次方数
题目描述
在你的帮助下,v神终于帮同学找到了最合适的大学,接下来就要通知同学了。在班级里负责联络网的是dm同学,于是v神便找到了dm同学,可dm同学正在忙于研究一道有趣的数学题,为了请dm出山,v神只好请你帮忙解决这道题了。
题目描述:将一个整数m分解为n个四次方数的和的形式,要求n最小。例如,m=706,706=5^4+3^4,则n=2。
输入格式
一行,一个整数m。
输出格式
一行,一个整数n。
输入输出样例
输入 #1复制
706
输出 #1复制
2
说明/提示
数据范围:对于30%的数据,m<=5000;对于100%的数据,m<=100,000
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int m, dp[100010], a[100010];
int main()
{
cin >> m;
int cnt;
memset(dp, 60, sizeof(dp));
dp[0] = 0;
for (int i = 1; i <= m; i++)
{
a[i] = pow(i, 4);
if (a[i] > m)
{
cnt = i;
break;
}
}
for (int i = 1; i <= cnt; i++)
{
for (int j = a[i]; j <= m; j++)
{
dp[j] = min(dp[j], dp[j - a[i]] + 1);
}
}
cout << dp[m];
return 0;
}
10.P1757 通天之分组背包
题目描述
自 01背包问世之后,小 A 对此深感兴趣。一天,小 A 去远游,却发现他的背包不同于 01 背包,他的物品大致可分为 k组,每组中的物品相互冲突,现在,他想知道最大的利用价值是多少。
输入格式
两个数 m,n,表示一共有 nn 件物品,总重量为 mm。
接下来 n 行,每行 3个数 a_i,b_i,c_i,表示物品的重量,利用价值,所属组数。
输出格式
一个数,最大的利用价值。
输入输出样例
输入 #1复制
45 3
10 10 1
10 5 1
50 400 2
输出 #1复制
10
代码
#include <iostream>
using namespace std;
int m, n, dp[1010];
struct bag
{
int tat;
int w[1010];
int v[1010];
}a[1010];
int main()
{
cin >> m >> n;
int cnt = 0;
for (int i = 1; i <= n; i++)
{
int x, y, z;
cin >> x >> y >> z;
cnt = max(cnt, z); //组数
a[z].tat++; //组内的数量
a[z].w[a[z].tat] = x;
a[z].v[a[z].tat] = y;
}
for (int i = 1; i <= cnt; i++)
{
for (int j = m; j >= 0; j--)
{
for (int k = 1; k <= a[i].tat; k++)
{
if (j - a[i].w[k] >= 0)
dp[j] = max(dp[j], dp[j - a[i].w[k]] + a[i].v[k]);
}
}
}
cout << dp[m];
return 0;
}
11.P1064 [NOIP2006 提高组] 金明的预算方案
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 nn 元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
| 主件 | 附件 |
| :—-: | :————: |
| 电脑 | 打印机,扫描仪 |
| 书柜 | 图书 |
| 书桌 | 台灯,文具 |
| 工作椅 | 无 |
如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 00 个、11 个或 22 个附件。每个附件对应一个主件,附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的 nn 元。于是,他把每件物品规定了一个重要度,分为 55 等:用整数 1 \sim 51∼5 表示,第 55 等最重要。他还从因特网上查到了每件物品的价格(都是 1010 元的整数倍)。他希望在不超过 nn 元的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 jj 件物品的价格为 v_jvj,重要度为w_jwj,共选中了 kk 件物品,编号依次为 j_1,j_2,\dots,j_kj1,j2,…,jk,则所求的总和为:
v_{j_1} \times w_{j_1}+v_{j_2} \times w_{j_2}+ \dots +v_{j_k} \times w_{j_k}vj1×wj1+vj2×wj2+⋯+vjk×wjk。
请你帮助金明设计一个满足要求的购物单。
输入格式
第一行有两个整数,分别表示总钱数 nn 和希望购买的物品个数 mm。
第 22 到第 (m + 1)(m+1) 行,每行三个整数,第 (i + 1)(i+1) 行的整数 v_ivi,p_ipi,q_iqi 分别表示第 ii 件物品的价格、重要度以及它对应的的主件。如果 q_i=0qi=0,表示该物品本身是主件。
输出格式
输出一行一个整数表示答案。
输入输出样例
输入 #1复制
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出 #1复制
2200
说明/提示
数据规模与约定
对于全部的测试点,保证 1 \leq n \leq 3.2 \times 10^41≤n≤3.2×104,1 \leq m \leq 601≤m≤60,0 \leq v_i \leq 10^40≤vi≤104,1 \leq p_i \leq 51≤pi≤5,0 \leq q_i \leq m0≤qi≤m,答案不超过 2 \times 10^52×105。
代码
#include <iostream>
using namespace std;
int n, m, dp[100010];
struct bag
{
int tot;
int p[5]; //总共有4种可能
int v[5];
}a[100];
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int x, y, z;
cin >> x >> y >> z;
if (z == 0)
{
a[i].tot = 1;
a[i].p[1] = x;
a[i].v[1] = x * y;
}
else
{
if (a[z].tot == 1)
{
a[z].p[2] = a[z].p[1] + x; //因为题目说最多两个附件,一个个放进去后面再dp的时候算最优的就行了
a[z].v[2] = a[z].v[1] + x * y;
a[z].tot = 2;
}
else
{
a[z].p[3] = a[z].p[1] + x;
a[z].v[3] = a[z].v[1] + x * y;
a[z].p[4] = a[z].p[2] + x;
a[z].v[4] = a[z].v[2] + x * y;
a[z].tot = 4;
}
}
}
for (int i = 1; i <= m; i++)
{
for (int j = n; j >= 0; j--)
{
for (int k = 1; k <= a[i].tot; k++) //分组背包噢
{
if (j - a[i].p[k] >= 0) //这个别忘了
dp[j] = max(dp[j], dp[j - a[i].p[k]] + a[i].v[k]);
}
}
}
cout << dp[n];
return 0;
}
高精度算法
前言
参考视频教程 洛谷 普及组试炼场 – 高精度算法
理解高精度算法,当题目数据规模过大时可能就需要考虑高精度解决了,高精度一般是通过数组输出~
以简单基础普及题型为例,可在洛谷上查找题目提交,代码仅供参考。
题目列表:
1.P1601 A+B Problem
2.P2142 高精度减法
3.P1303 A*B Problem
4.P1255 数楼梯
5.P1604 B进制星球
6.P1045 麦森数
7.算法提高 快速幂+取模
1.P1601 A+B Problem(高精)
题目描述
高精度加法,相当于a+b problem,不用考虑负数.
输入格式
分两行输入。a,b \leq 10^{500}a,b≤10500
输出格式
输出只有一行,代表a+ba+b的值
输入输出样例
输入 #1复制
1
1
输出 #1复制
2
输入 #2复制
1001
9099
输出 #2复制
10100
代码
#include <iostream>
#include <string>
using namespace std;
string aa,bb; //可能超过long long 得string输入
int a[10000010],b[10000010],c[10000010],la,lb,lc;
int main()
{
cin>>aa>>bb;
la = aa.length();
lb = bb.length();
for(int i=aa.length()-1;i>=0;i--)
{
a[aa.length()-i] = aa[i] - '0';
}
for(int i=bb.length()-1;i>=0;i--)
{
b[bb.length()-i] = bb[i] - '0';
}
lc = max(la,lb);
for(int i = 1 ; i <= lc; i++)
{
c[i] += a[i] +b[i]; //必须是 += , 防止漏了进位的数
c[i+1] = c[i]/10; //是否进位
c[i]%=10; //取余
}
if(c[lc+1]>0) //这里是判断是否最高位进位
lc++;
for(int i=lc;i>=1;i--)
{
cout<<c[i];
}
}
2.P2142 高精度减法
题目描述
高精度减法。
输入格式
两个整数 a,ba,b(第二个可能比第一个大)。
输出格式
结果(是负数要输出负号)。
输入输出样例
输入 #1复制
2
1
输出 #1复制
1
代码
#include <iostream>
#include <string>
#include <bits/stdc++.h>
using namespace std;
string aa, bb; //可能超过long long 得string输入
int a[10000010], b[10000010], c[10000010], la, lb, lc;
int main()
{
cin >> aa >> bb;
la = aa.length();
lb = bb.length();
if (la < lb || (la == lb && aa < bb)) //判断 aa,bb 的大小,当长度一致时string可以判断大小
{
swap(aa, bb);
swap(la, lb);
cout << "-";
}
for (int i = aa.length() - 1; i >= 0; i--)
{
a[aa.length() - i] = aa[i] - '0';
}
for (int i = bb.length() - 1; i >= 0; i--)
{
b[bb.length() - i] = bb[i] - '0';
}
for (int i = 1; i <= la; i++)
{
if (a[i] < b[i]) //当当前位为小于时
{
a[i] += 10;
a[i + 1]--;
}
c[i] = a[i] - b[i];
}
while (c[la] == 0 && la > 1) //判断前位是否为 0
la--;
for (int i = la; i >= 1; i--)
{
cout << c[i];
}
}
3.P1303 A*B Problem
题目描述
求两数的积。
输入格式
两行,两个整数。
输出格式
一行一个整数表示乘积。
输入输出样例
输入 #1复制
1
2
输出 #1复制
2
说明/提示
每个数字不超过 10^{2000}102000 ,需用高精。
代码
#include <iostream>
#include <string>
#include <bits/stdc++.h>
using namespace std;
string aa, bb; //可能超过long long 得string输入
int a[10000010], b[10000010], c[10000010], la, lb, lc;
int main()
{
cin >> aa >> bb;
la = aa.length();
lb = bb.length();
if (aa[0] == '-' && bb[0] != '-' || bb[0] == '-' && aa[0] != '-') //貌似不需要
{
cout << "-";
}
for (int i = aa.length() - 1; i >= 0; i--)
{
a[aa.length() - i] = aa[i] - '0';
}
for (int i = bb.length() - 1; i >= 0; i--)
{
b[bb.length() - i] = bb[i] - '0';
}
for (int i = 1; i <= la; i++)
{
for (int j = 1; j <= lb; j++)
{
c[i + j - 1] += a[i] * b[j];
c[i + j] += c[i + j - 1] / 10;
c[i + j - 1] %= 10;
}
}
lc = la + lb;
while (c[lc] == 0 && lc > 1) //判断前位是否为 0
lc--;
for (int i = lc; i >= 1; i--)
{
cout << c[i];
}
}
4.P1255 数楼梯
题目描述
楼梯有 N 阶,上楼可以一步上一阶,也可以一步上二阶。
编一个程序,计算共有多少种不同的走法。
输入格式
一个数字,楼梯数。
输出格式
输出走的方式总数。
输入输出样例
输入 #1复制
4
输出 #1复制
5
说明/提示
- 对于 60\%60% 的数据,N*≤50;
- 对于 100\%100% 的数据,N≤5000。
代码
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int a[500050], b[500050], c[500050], lc = 1; //lc 为位数
int main() //好好想想题目描述,会发现跟斐波那契数列差不多,看数据规模会发现可能需要用到高精度解决的方法
{
int n;
cin >> n;
// int a = 1,b=2,c; //下面方法的前身,当不用数组时的斐波那契数列可以这样表示
// for(int i=3;i<=n;i++)
// {
// c=a+b;
// a=b;
// b=c;
// }
// cout<<c;
a[1] = 1;
b[1] = 2;
for (int i = 3; i <= n; i++)
{
memset(c, 0, sizeof(c)); //每次都需要对 c 重新清零
for (int j = 1; j <= lc; j++)
{
c[j] += a[j] + b[j];
c[j + 1] += c[j] / 10;
c[j] = c[j] % 10;
}
if (c[lc + 1] > 0)
lc++;
for (int j = 1; j <= lc; j++)
{
a[j] = b[j];
}
for (int j = 1; j <= lc; j++)
{
b[j] = c[j];
}
}
if (n >= 3)
{
for (int i = lc; i >= 1; i--)
{
cout << c[i];
}
}
else if (n < 3)
{
switch (n)
{
case 0:cout << "0"; break; //别忘了 break !!
case 1:cout << "1"; break;
case 2:cout << "2"; break;
}
}
return 0;
}
5.P1604 B进制星球
题目背景
进制题目,而且还是个计算器~~
题目描述
话说有一天,小Z乘坐宇宙飞船,飞到一个美丽的星球。因为历史的原因,科技在这个美丽的星球上并不很发达,星球上人们普遍采用B(2<=B<=36)进制计数。星球上的人们用美味的食物招待了小Z,作为回报,小Z希望送一个能够完成B进制加法的计算器给他们。 现在小Z希望你可以帮助他,编写实现B进制加法的程序。
输入格式
共3行第1行:一个十进制的整数,表示进制B。第2-3行:每行一个B进制数正整数。数字的每一位属于{0,1,2,3,4,5,6,7,8,9,A,B……},每个数字长度<=2000位。
输出格式
一个B进制数,表示输入的两个数的和。
输入输出样例
输入 #1复制
4
123
321
输出 #1复制
1110
代码
#include <iostream>
#include <string>
using namespace std;
string aa, bb;
int a[300020], b[300020], c[300020], la, lb, lc = 1;
int main()
{
int n;
cin >> n;
cin >> aa >> bb;
la = aa.length();
lb = bb.length();
for (int i = la - 1; i >= 0; i--)
{
if (aa[i] >= 'A')
{
a[la - i] = aa[i] - 'A' + 10; //需要注意大于10进制的情况
}
else
{
a[la - i] = aa[i] - '0';
}
}
for (int i = lb - 1; i >= 0; i--)
{
if (bb[i] >= 'A')
{
b[lb - i] = bb[i] - 'A' + 10;
}
else
{
b[lb - i] = bb[i] - '0';
}
}
lc = max(la, lb);
for (int i = 1; i <= lc; i++)
{
c[i] += a[i] + b[i];
c[i + 1] = c[i] / n;
c[i] = c[i] % n;
}
if (c[lc + 1] > 0)
lc++;
for (int i = lc; i >= 1; i--)
{
if (c[i] >= 10)
{
cout << char(c[i] + 'A' - 10);
}
else
{
cout << c[i];
}
}
return 0;
}
6.P1045 麦森数
题目描述
形如2^P-1的素数称为麦森数,这时PP一定也是个素数。但反过来不一定,即如果PP是个素数,2^P-1不一定也是素数。到1998年底,人们已找到了37个麦森数。最大的一个是P=3021377,它有909526位。麦森数有许多重要应用,它与完全数密切相关。
任务:从文件中输入P(1000<P<3100000),计算2^P-1的位数和最后500位数字(用十进制高精度数表示)
输入格式
文件中只包含一个整数P(1000<P<3100000)
输出格式
第一行:十进制高精度数2^P-1的位数。
第2-11行:十进制高精度数2^P-1的最后500位数字。(每行输出50位,共输出10行,不足500位时高位补0)
不必验证2^P-1与P是否为素数。
输入输出样例
输入 #1复制
1279
输出 #1
386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int m[1010];
int a[1010];
int temp[1010]; //要有个临时保存的
void xianchen()
{
memset(temp, 0, sizeof(temp));
for (int i = 1; i <= 500; i++) //直接500给他
{
for (int j = 1; j <= 500; j++)
{
temp[i + j - 1] += m[i] * a[j];
temp[i + j] += temp[i + j - 1] / 10;
temp[i + j - 1] %= 10;
}
}
memcpy(m, temp, sizeof(m)); //把 temp 的值传给 m
}
void zichen()
{
memset(temp, 0, sizeof(temp));
for (int i = 1; i <= 500; i++)
{
for (int j = 1; j <= 500; j++)
{
temp[i + j - 1] += a[i] * a[j];
temp[i + j] += temp[i + j - 1] / 10;
temp[i + j - 1] %= 10;
}
}
memcpy(a, temp, sizeof(a));
}
int main()
{
long long p;
cin >> p;
cout << int((p * log10(2)) + 1) << endl; //求位数可以通过 log10()+1 解决
a[1] = 2;
m[1] = 1;
while (p != 0)
{
if (p % 2 == 1)
{
xianchen();
}
p /= 2;
zichen();
}
m[1]--;
for (int i = 500; i >= 1; i--)
{
if (i % 50 == 0 && i != 500)
{
cout << endl;
}
cout << m[i];
}
}
7.算法提高 快速幂+取模
问题描述
给定A, B, P,求(A^B) mod P。
输入格式
输入共一行。
第一行有三个数,N, M, P。
输出格式
输出共一行,表示所求。
样例输入
2 5 3
样例输出
2
数据规模和约定
共10组数据
对100%的数据,A, B为long long范围内的非负整数,P为int内的非负整数。
代码
#include<iostream>
using namespace std;
int main()
{
long long a, b;
int p;
cin >> a >> b >> p;
long long ans = 1;
a %= p;
while (b != 0)
{
if (b & 1) //即 b%2==1 ,可以加快速度
{
ans = (ans * a) % p;
}
a = (a * a) % p;
b >>= 1; // 即 b /= 2;
}
cout << ans << endl;
}
贪心
前言
参考视频教程 https://www.bilibili.com/video/BV1hE411773n?p=3
有就要
以简单基础普及题型为例,可在洛谷上查找题目提交,代码仅供参考。
题目列表:
1.P1181 数列分段 Section I
2.P1094 [NOIP2007 普及组] 纪念品分组
3.P1208 [USACO1.3]混合牛奶 Mixing Milk
1.P1181 数列分段 Section I
题目描述
对于给定的一个长度为NN的正整数数列A_iAi,现要将其分成连续的若干段,并且每段和不超过MM(可以等于MM),问最少能将其分成多少段使得满足要求。
输入格式
第1行包含两个正整数N,MN,M,表示了数列A_iAi的长度与每段和的最大值,第22行包含NN个空格隔开的非负整数A_iAi,如题目所述。
输出格式
一个正整数,输出最少划分的段数。
输入输出样例
输入 #1复制
5 6
4 2 4 5 1
输出 #1复制
3
说明/提示
对于20\%20%的数据,有N≤10N≤10;
对于40\%40%的数据,有N≤1000N≤1000;
对于100\%100%的数据,有N≤100000,M≤10^9N≤100000,M≤109,MM大于所有数的最小值,A_iAi之和不超过10^9109。
将数列如下划分:
[4][2 4][5 1][4][24][51]
第一段和为44,第22段和为66,第33段和为66均满足和不超过M=6M=6,并可以证明33是最少划分的段数。
代码
#include<iostream>
using namespace std;
int main()
{
int n, m;
cin >> n >> m;
int sum = 0;
int cnt = 1;
while (n--)
{
int temp;
cin >> temp;
if (sum + temp <= m)
{
sum += temp;
}
else
{
cnt++;
sum = temp;
}
}
cout << cnt;
return 0;
}
2.P1094 [NOIP2007 普及组] 纪念品分组
题目描述
元旦快到了,校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得 的纪念品价值相对均衡,他要把购来的纪念品根据价格进行分组,但每组最多只能包括两件纪念品, 并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品,乐乐希望分组的数目最少。
你的任务是写一个程序,找出所有分组方案中分组数最少的一种,输出最少的分组数目。
输入格式
共 n+2n+2 行:
第一行包括一个整数 ww,为每组纪念品价格之和的上上限。
第二行为一个整数 nn,表示购来的纪念品的总件数 GG。
第 3\sim n+23∼n+2 行每行包含一个正整数 P_iPi 表示所对应纪念品的价格。
输出格式
一个整数,即最少的分组数目。
输入输出样例
输入 #1复制
100
9
90
20
20
30
50
60
70
80
90
输出 #1复制
6
说明/提示
50\%50% 的数据满足:1\le n\le151≤n≤15。
100\%100% 的数据满足:1\le n\le3\times10^41≤n≤3×104,80\le w\le20080≤w≤200,5 \le P_i \le w5≤Pi≤w。
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int a[300010];
int main()
{
int w, n;
cin >> w >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
int l = 1;
sort(a + 1, a + n + 1);
int cnt = 0;
while (l <= n)
{
if (a[l] + a[n] <= w)
{
l++;
n--;
cnt++;
}
else
{
n--;
cnt++;
}
}
cout << cnt;
return 0;
}
3.P1208 [USACO1.3]混合牛奶 Mixing Milk
题目描述
由于乳制品产业利润很低,所以降低原材料(牛奶)价格就变得十分重要。帮助 Marry 乳业找到最优的牛奶采购方案。
Marry 乳业从一些奶农手中采购牛奶,并且每一位奶农为乳制品加工企业提供的价格是不同的。此外,就像每头奶牛每天只能挤出固定数量的奶,每位奶农每天能提供的牛奶数量是一定的。每天 Marry 乳业可以从奶农手中采购到小于或者等于奶农最大产量的整数数量的牛奶。
给出 Marry 乳业每天对牛奶的需求量,还有每位奶农提供的牛奶单价和产量。计算采购足够数量的牛奶所需的最小花费。
注:每天所有奶农的总产量大于 Marry 乳业的需求量。
输入格式
第一行二个整数 n,mn,m,表示需要牛奶的总量,和提供牛奶的农民个数。
接下来 mm 行,每行两个整数 p_i,a_ipi,ai,表示第 ii 个农民牛奶的单价,和农民 ii 一天最多能卖出的牛奶量。
输出格式
单独的一行包含单独的一个整数,表示 Marry 的牛奶制造公司拿到所需的牛奶所要的最小费用。
输入输出样例
输入 #1复制
100 5
5 20
9 40
3 10
8 80
6 30
输出 #1复制
630
说明/提示
【数据范围】
对于 100\%100% 的数据:
0 \le n,a_i \le 2 \times 10^60≤n,ai≤2×106,0\le m \le 50000≤m≤5000,0 \le p_i \le 10000≤pi≤1000
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
struct row
{
int m;
int l;
};
bool cmp(row a, row b)
{
return a.m < b.m;
}
int main()
{
int n, m;
cin >> n >> m;
row a[5020];
for (int i = 1; i <= m; i++)
cin >> a[i].m >> a[i].l;
sort(a + 1, a + m + 1, cmp);
int sum = 0;
for (int i = 1; i <= m; i++)
{
if (n >= a[i].l)
{
n -= a[i].l;
sum += a[i].l * a[i].m;
}
else
{
sum += n * a[i].m;
break;
}
}
cout << sum;
return 0;
}
理解字符串处理基础题
前言
参考视频教程 https://www.bilibili.com/video/BV1W7411s728?p=4
以一些基础简单字符串处理题展开练习了解,掌握一些小小技巧。
以简单基础普及题型为例,可在洛谷上查找题目提交,代码仅供参考。
题目列表:
1.P1603 斯诺登的密码
2.P1071 [NOIP2009 提高组] 潜伏者
3.P1012 [NOIP1998 提高组] 拼数
4.P1538 迎春舞会之数字舞蹈
1.P1603 斯诺登的密码
题目描述
2013 年 X 月 X 日,俄罗斯办理了斯诺登的护照,于是他混迹于一架开往委内瑞拉的飞机。但是,这件事情太不周密了,因为FBI的间谍早已获悉他的具体位置——但这不是最重要的——最重要的是如果要去委内瑞拉,那么就要经过古巴,而经过古巴的路在美国的掌控之中。
丧心病狂的奥巴马迫降斯诺登的飞机,搜查时却发现,斯诺登杳无踪迹。但是,在据说是斯诺登的座位上,发现了一张纸条。纸条由纯英文构成:Obama is a two five zero.(以 . 结束输出,只有 6 个单词+一个句号,句子开头如没有大写亦为合法)这句话虽然有点无厘头,但是警官陈珺骛发现这是一条极其重要的线索。他在斯诺登截获的一台笔记本中找到了一个 C++ 程序,输入这条句子后立马给出了相对应的密码。陈珺鹜高兴得晕了过去,身为警官的你把字条和程序带上了飞机,准备飞往曼哈顿国际机场,但是在飞机上检查的时候发现——程序被粉碎了!飞机抵达华盛顿只剩5分钟,你必须在这 5 分钟内编写(杜撰)一个程序,免受上司的 10000000000%10 大板。破译密码的步骤如下:
(1)找出句子中所有用英文表示的数字(\leq 20)(≤20),列举在下:
正规:one two three four five six seven eight nine ten eleven twelve thirteen fourteen fifteen sixteen seventeen eighteen nineteen twenty
非正规:a both another first second third。为避免造成歧义,another 算作 11 处理。
(2)将这些数字平方后对 100100 取模,如 00,05,11,19,86,9900,05,11,19,86,99。
(3)把这些两位数按数位排成一行,组成一个新数,如果开头为 00,就去 00。
(4)找出所有排列方法中最小的一个数,即为密码。
// 数据已经修正 By absi2011 如果还有问题请联系我
输入格式
一个含有 6 个单词的句子。
输出格式
一个整型变量(密码)。如果没有符合要求的数字出现,则输出 0。
输入输出样例
输入 #1复制
Black Obama is two five zero .
输出 #1复制
425
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
string word[] = { "one","two","three","four","five","six","seven","eight","nine","ten","eleven","twelve","thirteen","fourteen","fifteen","sixteen","seventeen","eighteen","nineteen","twenty","a","both","another","first","second","third" };
int a[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,1,2,1,1,2,3 }; //用这个方法主要是想学习up的那个 ctrl+F 操作,其实也可以map操作
int b[100];
string temp;
int n;
int main()
{
for (int i = 0; i < 6; i++)
{
cin >> temp;
for (int j = 0; j < 26; j++)
{
if (word[j] == temp)
{
b[++n] = a[j];
b[n] *= b[n];
b[n] %= 100;
}
}
}
sort(b + 1, b + n + 1);
if (n == 0)
{
cout << "0";
return 0;
}
cout << b[1];
for (int i = 2; i <= n; i++)
{
if (b[i] < 10)
{
cout << "0";
}
cout << b[i];
}
return 0;
}
2.P1071 [NOIP2009 提高组] 潜伏者
题目描述
RR国和SS国正陷入战火之中,双方都互派间谍,潜入对方内部,伺机行动。历尽艰险后,潜伏于SS国的RR 国间谍小CC终于摸清了 SS 国军用密码的编码规则:
1. SS国军方内部欲发送的原信息经过加密后在网络上发送,原信息的内容与加密后所得的内容均由大写字母‘A-Z’构成(无空格等其他字符)。
2. SS国对于每个字母规定了对应的“密字”。加密的过程就是将原信息中的所有字母替换为其对应的“密字”。
3. 每个字母只对应一个唯一的“密字”,不同的字母对应不同的“密字”。“密字”可以和原字母相同。
例如,若规定‘AA’的密字为‘A‘,‘B’的密字为‘C’(其他字母及密字略),则原信息“ABA”被加密为“ACA”。
现在,小CC 通过内线掌握了SS 国网络上发送的一条加密信息及其对应的原信息。小CC希望能通过这条信息,破译SS 国的军用密码。小 CC 的破译过程是这样的:扫描原信息,对于原信息中的字母xx(代表任一大写字母),找到其在加密信息中的对应大写字母yy,并认为在密码里 yy是xx的密字。如此进行下去直到停止于如下的某个状态:
1. 所有信息扫描完毕,A-Z’所有 2626个字母在原信息中均出现过并获得了相应的“密字”。
2. 所有信息扫描完毕,但发现存在某个(或某些)字母在原信息中没有出现。
3. 扫描中发现掌握的信息里有明显的自相矛盾或错误(违反 SS 国密码的编码规则)。例
如某条信息“XYZ”被翻译为“ABA”就违反了“不同字母对应不同密字”的规则。
在小 CC 忙得头昏脑涨之际,RR 国司令部又发来电报,要求他翻译另外一条从 SS国刚刚截取到的加密信息。现在请你帮助小CC:通过内线掌握的信息,尝试破译密码。然后利用破译的密码,翻译电报中的加密信息。
输入格式
共 33行,每行为一个长度在 11到 100100之间的字符串。
第 11 行为小 CC 掌握的一条加密信息。
第22 行为第 11 行的加密信息所对应的原信息。
第 33行为 RR国司令部要求小C翻译的加密信息。
输入数据保证所有字符串仅由大写字母‘A-Z’构成,且第 11行长度与第 22行相等。
输出格式
共 11 行。
若破译密码停止时出现 2,32,3 两种情况,请你输出“Failed”(不含引号,注意首字母大
写,其它小写)。
否则请输出利用密码翻译电报中加密信息后得到的原信息。
输入输出样例
输入 #1复制
AA
AB
EOWIE
输出 #1复制
Failed
输入 #2复制
QWERTYUIOPLKJHGFDSAZXCVBN
ABCDEFGHIJKLMNOPQRSTUVWXY
DSLIEWO
输出 #2复制
Failed
输入 #3复制
MSRTZCJKPFLQYVAWBINXUEDGHOOILSMIJFRCOPPQCEUNYDUMPP
YIZSDWAHLNOVFUCERKJXQMGTBPPKOIYKANZWPLLVWMQJFGQYLL
FLSO
输出 #3复制
NOIP
说明/提示
【输入输出样例11说明】
原信息中的字母‘AA’和‘BB’对应相同的密字,输出“Failed”。
【输入输出样例 22说明】
字母‘ZZ’在原信息中没有出现,输出“Failed”。
代码
#include <iostream>
#include <string>
#include <map>
using namespace std;
int main()
{
string a, b;
map<char, char>mp; //这题没啥难度,开两个map分别密码对密文,密文对明文就行了
map<char, char>mp2;
cin >> a >> b;
string c;
cin >> c;
int flag = 0;
for (int i = 0; i < a.length(); i++)
{
if (mp.count(a[i]) == 0)
{
if (mp2.count(b[i]) == 0)
{
mp2[b[i]] = a[i];
}
else if (mp2[b[i]] != a[i])
{
cout << "Failed";
return 0;
}
mp[a[i]] = b[i];
flag++;
}
else if (mp.count(a[i]) != 0 && mp[a[i]] != b[i])
{
cout << "Failed";
return 0;
}
}
if (flag != 26)
{
cout << "Failed";
return 0;
}
for (int i = 0; i < c.length(); i++)
{
cout << mp[c[i]];
}
return 0;
}
3.P1012 [NOIP1998 提高组] 拼数
题目描述
设有 n个正整数 a_1 \dots a_na1…an,将它们联接成一排,相邻数字首尾相接,组成一个最大的整数。
输入格式
第一行有一个整数,表示数字个数 n。
第二行有 n个整数,表示给出的 n 个整数 a_i。
输出格式
一个正整数,表示最大的整数
输入输出样例
输入 #1复制
3
13 312 343
输出 #1复制
34331213
输入 #2复制
4
7 13 4 246
输出 #2复制
7424613
说明/提示
对于全部的测试点,保证 1 \leq n \leq 201≤n≤20,1 \leq a_i \leq 10^91≤ai≤109。
代码
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
bool cmp(string a, string b)
{
return a + b > b + a; //防止 915、91出现 91591 这种情况,应该为 91915
}
int main()
{
// string test1="110";
// string test2="1101"; //按第一位开始比 ,当前面一样时,长度长的大
// if(test1<test2)
// {
// cout<<test1<<"<"<<test2<<endl;
// }else if(test1>test2)
// {
// cout<<test1<<">"<<test2<<endl;
// }else
// {
// cout<<test1<<"="<<test2<<endl;
// }
int n;
cin >> n;
string a[n];
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
sort(a, a + n, cmp);
for (int i = 0; i < n; i++)
{
cout << a[i];
}
}
4.P1538 迎春舞会之数字舞蹈
题目描述
在越来越讲究合作的时代,人们注意的更多的不是个人物的舞姿,而是集体的排列。
为了配合每年的倒计时,同学们决定排出——“数字舞蹈”。顾名思义就是所有人一起排成若干个数字 -___-|||| 更为创新的是,每个人都是趴在地上,保证横竖。
现在给出数字及其要求摆出的大小,请你编程,模拟同学们的优美姿态。
输入格式
第一行为k。k表示要摆出数字的大小。
第二行为全部由数字组成的字符串,即要摆出的几个数字。
输出格式
按题目要求输出。
输入输出样例
输入 #1复制
2
1234567890
输出 #1复制
-- -- -- -- -- -- -- --
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
-- -- -- -- -- -- --
| | | | | | | | | | | | |
| | | | | | | | | | | | |
-- -- -- -- -- -- --
说明/提示
除了第一个数字之外,每个数字之前有1个空格,所有数字全部对齐。 //这里说明在每个数字后面加空格~
k<=30,s的长度不超过255
建议大家直接输出,不要保存。
如果对于大小和k有疑问,请自行理解。
代码
#include <iostream>
#include <string>
using namespace std;
int k;
string nums;
string a[5]={
" - - - - - - - - ",
"| | | | | | | | | | | | | | ",
" - - - - - - - ",
"| | | | | | | | | | | | | ",
" - - - - - - - ",
};
char f(int x,int y)
{
// if(x>0) x = max(x-(k-1),1);
// if(x>=3) x = max(x-(k-1),3);
// int m = y/(k+3);
// y%=(k+3);
// if(y>0) y=max(y-(k-1),1);
// return a[x][y+(nums[m]-'0')*4];
if(x>0&&x<=k) //上面方法的好理解处理,让坐标对应基础坐标
x=1;
if(x==k+1)
x=2;
if(x>k+1&&x<=k+1+k)
x=3;
if(x>k+1+k)
x=4;
int m = y/(k+3); //需要知道 y 对应的是原字符串的哪个位置
y = y%(k+3); //对应哪个位置
if(y>0&&y<=k)
y=1;
if(y==k+1)
y=2;
if(y>k+1)
y=3;
return a[x][y+(nums[m]-'0')*4];
}
int main()
{
cin>>k>>nums;
int h = k*2+3;
int w = (k+3)*nums.length();
for(int i = 0; i<h;i++)
{
for(int j=0;j<w;j++)
{
cout<<f(i,j);
}
cout<<endl;
}
return 0;
}
带有技巧的搜索
前言
参考视频教程 https://www.bilibili.com/video/BV14E411q73d?p=3
有技巧的搜索。
以简单基础普及题型为例,可在洛谷上查找题目提交,代码仅供参考。
题目列表:
1.P1118 [USACO06FEB]Backward Digit Sums G/S-涉及杨辉三角
2.P1434 [SHOI2002]滑雪
3.P1433 吃奶酪
4.P1784 数独
1.P1118 [USACO06FEB]Backward Digit Sums G/S-涉及杨辉三角
题目描述
有这么一个游戏:
写出一个11至NN的排列ai,然后每次将相邻两个数相加,构成新的序列,再对新序列进行这样的操作,显然每次构成的序列都比上一次的序列长度少1,直到只剩下一个数字位置。下面是一个例子:
3,1,2,4
4,3,6
7,9
16
最后得到1616这样一个数字。
现在想要倒着玩这样一个游戏,如果知道N,知道最后得到的数字的大小sum,请你求出最初序列ai,为1至N的一个排列。若答案有多种可能,则输出字典序最小的那一个。
管理员注:本题描述有误,这里字典序指的是1,2,3,4,5,6,7,8,9,10,11,12
而不是1,10,11,12,2,3,4,5,6,7,8,9
输入格式
两个正整数n,sum。
输出格式
输出包括1行,为字典序最小的那个答案。
当无解的时候,请什么也不输出。(好奇葩啊)
输入输出样例
输入 #1复制
4 16
输出 #1复制
3 1 2 4
说明/提示
对于40%的数据,n≤7;
对于80%的数据,n≤10;
对于100%的数据,n≤12,sum≤12345。
代码
#include <iostream>
using namespace std;
int n, m, y[15][15];
int a[15]; //记录路径
int vis[15];//记录数字使用情况
int flag = 0;
void dfs(int wz, int s)
{
if (flag == 1)
{
return;
}
if (s > m || wz > n + 1)
{
return;
}
if (wz == n + 1)
{
if (s == m)
{
for (int i = 1; i <= n; i++)
{
cout << a[i] << " ";
}
flag = 1;
}
return;
}
for (int i = 1; i <= n; i++)
{
if (vis[i] == 0)
{
vis[i] = 1;
a[wz] = i;
dfs(wz + 1, s + y[n][wz] * i);
vis[i] = 0;
}
}
}
int main()
{
cin >> n >> m;
y[1][1] = 1;
for (int i = 2; i <= 13; i++) //构建杨辉三角
{
for (int j = 1; j <= i; j++)
{
y[i][j] = y[i - 1][j - 1] + y[i - 1][j];
}
}
dfs(1, 0);
return 0;
}
2.P1434 [SHOI2002]滑雪
题目描述
Michael 喜欢滑雪。这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度会减小。在上面的例子中,一条可行的滑坡为 2424-1717-1616-11(从 2424 开始,在 11 结束)。当然 2525-2424-2323-\ldots…-33-22-11 更长。事实上,这是最长的一条。
输入格式
输入的第一行为表示区域的二维数组的行数 R和列数 C。下面是 R行,每行有 C个数,代表高度(两个数字之间用 1个空格间隔)。
输出格式
输出区域中最长滑坡的长度。
输入输出样例
输入 #1复制
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
输出 #1复制
25
说明/提示
对于100% 的数据,1\leq R,C\leq 1001≤R,C≤100。
代码
#include <iostream>
using namespace std;
int r, c, a[110][110];
int xx[] = { -1,1,0,0 };
int yy[] = { 0,0,-1,1 };
int dp[110][110]; //每个点最高值记录
int dfs(int x, int y)
{
int maxn = 1;
if (dp[x][y] != 0) //当其它点搜索到这个已记录点,则可以直接返回,因为它已记录过最高点
{
return dp[x][y];
}
for (int i = 0; i < 4; i++)
{
int dx = x + xx[i];
int dy = y + yy[i];
if (dx >= 1 && dx <= r && dy >= 1 && dy <= c && a[dx][dy] < a[x][y])
{
maxn = max(maxn, dfs(dx, dy) + 1);
}
}
return dp[x][y] = maxn; //记忆化每个点最大高度
}
int main()
{
cin >> r >> c;
for (int i = 1; i <= r; i++)
{
for (int j = 1; j <= c; j++)
{
cin >> a[i][j];
}
}
int ans = 0;
for (int i = 1; i <= r; i++)
{
for (int j = 1; j <= c; j++)
{
ans = max(ans, dfs(i, j));
}
}
cout << ans;
return 0;
}
3.P1433 吃奶酪
题目描述
房间里放着 n块奶酪。一只小老鼠要把它们都吃掉,问至少要跑多少距离?老鼠一开始在 (0,0)点处。
输入格式
第一行有一个整数,表示奶酪的数量 n。
第 2到第 (n + 1)行,每行两个实数,第 (i + 1) 行的实数分别表示第 ii 块奶酪的横纵坐标 x_i, y_i。
输出格式
输出一行一个实数,表示要跑的最少距离,保留 2 位小数。
输入输出样例
输入 #1复制
4
1 1
1 -1
-1 1
-1 -1
输出 #1复制
7.41
说明/提示
数据规模与约定
对于全部的测试点,保证 1\leq n\leq 151≤n≤15,|x_i|, |y_i| \leq 200∣xi∣,∣yi∣≤200,小数点后最多有 33 位数字。
提示
对于两个点(x1,y1),(x2,y2),两点之间的距离公式为 \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}(x1−x2)2+(y1−y2)2。
代码
#include <iostream>
#include <iomanip>
#include <bits/stdc++.h>
using namespace std;
double n, x[20] = { 0 }, y[20] = { 0 }; //x,y[]记录每个奶酪的点
double minn = 10000000;
int vis[20];
double sqrtt(int q, int h)
{
return sqrt((x[h] - x[q]) * (x[h] - x[q]) + (y[h] - y[q]) * (y[h] - y[q]));
}
void dfs(int dq, double s, int cnt)
{
if (cnt == n)
{
minn = min(minn, s);
return;
}
if (s >= minn)
{
return;
}
for (int i = 1; i <= n; i++)
{
if (vis[i] == 0)
{
vis[i] = 1;
dfs(i, s + sqrtt(dq, i), cnt + 1);
vis[i] = 0;
}
}
}
int main() //最后一个案例超时,但现在不是很能理解老师解决的做法
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> x[i] >> y[i];
}
dfs(0, 0, 0);
cout << fixed << setprecision(2) << minn;
return 0;
}
4.P1784 数独
题目描述
数独是根据 9 \times 99×9 盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫内的数字均含 1 – 91−9 ,不重复。每一道合格的数独谜题都有且仅有唯一答案,推理方法也以此为基础,任何无解或多解的题目都是不合格的。
芬兰一位数学家号称设计出全球最难的“数独游戏”,并刊登在报纸上,让大家去挑战。
这位数学家说,他相信只有“智慧最顶尖”的人才有可能破解这个“数独之谜”。
据介绍,目前数独游戏的难度的等级有一到五级,一是入门等级,五则比较难。不过这位数学家说,他所设计的数独游戏难度等级是十一,可以说是所以数独游戏中,难度最高的等级。他还表示,他目前还没遇到解不出来的数独游戏,因此他认为“最具挑战性”的数独游戏并没有出现。
输入格式
一个未填的数独。
输出格式
填好的数独。
输入输出样例
输入 #1复制
8 0 0 0 0 0 0 0 0
0 0 3 6 0 0 0 0 0
0 7 0 0 9 0 2 0 0
0 5 0 0 0 7 0 0 0
0 0 0 0 4 5 7 0 0
0 0 0 1 0 0 0 3 0
0 0 1 0 0 0 0 6 8
0 0 8 5 0 0 0 1 0
0 9 0 0 0 0 4 0 0
输出 #1复制
8 1 2 7 5 3 6 4 9
9 4 3 6 8 2 1 7 5
6 7 5 4 9 1 2 8 3
1 5 4 2 3 7 8 9 6
3 6 9 8 4 5 7 2 1
2 8 7 1 6 9 5 3 4
5 2 1 9 7 4 3 6 8
4 3 8 5 2 6 9 1 7
7 9 6 3 1 8 4 5 2
代码
#include <iostream>
using namespace std;
int mp[11][11];
int vx[11][11]; //vx[i][j] i 代表第几行,j 代表当中哪个数字出现过
int vy[11][11]; //列
int va[11][11]; //区域内
void dfs(int x, int y)
{
if (y == 10)
{
dfs(x + 1, 1);
return;
}
if (x == 10)
{
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
cout << mp[i][j] << " ";
}
cout << endl;
}
return;
}
if (mp[x][y] != 0)
{
dfs(x, y + 1);
return;
}
for (int i = 1; i <= 9; i++)
{
if (vx[x][i] == 0 && vy[y][i] == 0 && va[(x - 1) / 3 * 3 + (y - 1) / 3 + 1][i] == 0)
{
vx[x][i] = 1;
vy[y][i] = 1;
va[(x - 1) / 3 * 3 + (y - 1) / 3 + 1][i] = 1;
mp[x][y] = i;
dfs(x, y + 1);
vx[x][i] = 0;
vy[y][i] = 0;
va[(x - 1) / 3 * 3 + (y - 1) / 3 + 1][i] = 0;
mp[x][y] = 0;
}
}
}
int main()
{
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
cin >> mp[i][j];
vx[i][mp[i][j]] = 1;
vy[j][mp[i][j]] = 1;
va[(i - 1) / 3 * 3 + (j - 1) / 3 + 1][mp[i][j]] = 1; //区域 1 2 3
// 4 5 6
}
}
dfs(1, 1);
return 0;
}